Lesson 3

Ellipses

In this lesson students will become familiar with the equations and graphs of ellipses. The definition of an ellipse will be learned both algebraically and using the distance relationship. Students will learn how to construct an ellipse using Geometer’s Sketchpad and how to prove that this construction is an ellipse. Applications of ellipses will be explored.

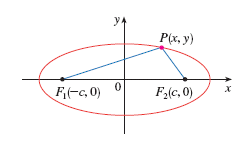
Definition: An ellipse is the set of all points P in a plane such that the sum of the distances from P to two fixed points, and , called the foci, is constant.

Some other important information includes the following:

· Major axis is represented by 2a and is the longest axis of the ellipse.

· Minor axis is represented by 2b and is the shortest axis of the ellipse.

· Eccentricity is the measure of how round or flat the ellipse is. It is the ratio of the distance from the center to a focus, and the distance from the center to a vertex. .

· The center of the ellipse is represented by (h, k).

· The relationship between a, b, and c, is a²-b²=c². For an exploration on why, click here.

· Standard equations for the ellipse and the graph of each are shown below.

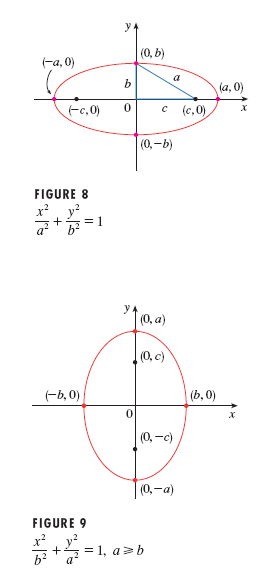
Note that when the center of the ellipse is translated to a point (h, k) so that the center is other than the origin, the equation will become

for figure 8, and for figure 9.

Try constructing an ellipse using GSP. First complete the wax paper folding activity. Use the instructions provided to complete this construction by clicking here. The ellipse that has been constructed is not necessarily oriented to the standard coordinate system. After your construction is complete, prove that the construction is an ellipse. Show your proof using two different methods, geometric and algebraic. Click here to explore the construction of an ellipse.

Practice problem 1: The moon orbits Earth in an elliptical path with the center of the Earth at one focus. The major axis of the orbit is 774,000 kilometers, and the minor axis is 773,000 kilometers.

1. Using (0, 0) as the center of the ellipse, write the standard equation for the orbit of the Moon around Earth.

2. How far from the center of Earth is the Moon at its closest point?

3. How far from the center of Earth is the Moon at its farthest point?

4. Find the eccentricity of the Moon’s orbit around Earth.

Practice problem 2: If the ellipse is defined by the equation 16x²+4y²+96x+8y+84=0 is translated 4 units down and 7 units to the left, write the standard equation of the resulting ellipse.