Lesson
5
Hyperbolas
In this
lesson students will become familiar with the equations and graphs of
hyperbolas. The definition of a
hyperbola will be learned both algebraically and using the distance
relationship. Students will learn how to
construct a hyperbola using Geometer’s Sketchpad and how to prove that this
construction is a hyperbola.
Applications of hyperbolas will be explored.
Definition: A
hyperbola is the set of points P(x, y)
in a plane such that the absolute value of the difference between the distances
from P to two fixed points in the
plane, F1 and F2, called the foci, is a
constant.
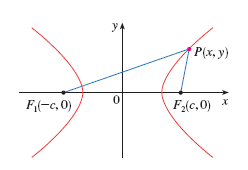
Some other important information includes the
following:
·
The center of the hyperbola is located
at (h, k).
·
The vertices are located on the
transverse axis. The length of the
transverse axis is 2a.
·
The co vertices are located on the
conjugate axis. The length of the
conjugate axis is 2b.
·
The foci are located on the transverse
axis a distance of c from the center.
·
The equations for the asymptotes of the
hyperbola are 
for a horizontal transverse axis hyperbola, and 
for a vertical transverse axis hyperbola.
·
The relationship between a, b, and c is a2+b2=c2.
Standard equations for the hyperbola
and the graph of each are shown below.
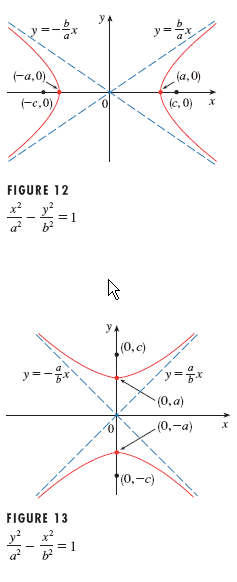
Note that when the center of the hyperbola is
translated to a point (h, k) so that
the center is other than the origin, the equation will become
for
figure 12, and 
for figure 13.
Try constructing a hyperbola using GSP. Use the instructions provided to complete this
construction by clicking here. After your construction is complete, prove
that the construction is a hyperbola.
Show your proof using two different methods, geometric and
algebraic. Click here to explore the construction of a hyperbola
on GSP. The hyperbola that has been
constructed is not necessarily oriented to the standard coordinate system.
Practice problem 1: An explosion is heard by two law enforcement officers who are
1000 meters apart. One officer heard the
explosion 1.5 seconds after the other officer.
The speed of sound in air (at 20 C) is approximately 340 meters per second. Write an equation for the possible locations
of the explosion, relative to the two law enforcement officers.
Practice problem 2: Translate the hyperbola defined by the equation 9x2-4y2+54x+8y+41=0
up 2 units and to the left 6 units.
Write the standard equation of the resulting hyperbola.
Practice problem 3: A telescope may have a hyperbolic mirror with
the property that a ray of light directed at one focus is reflected to the
other focus. If the center is located
at the origin, a focus has coordinates (5, 0), a vertex has coordinates (3, 0),
and one end of the mirror is attached to the telescope at the point (5, 16/3),
find the equation that defines the mirror.
Draw a diagram.