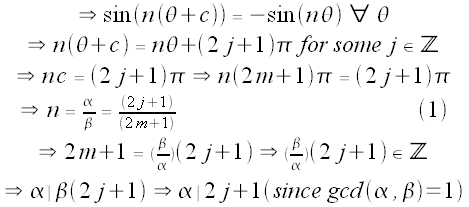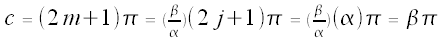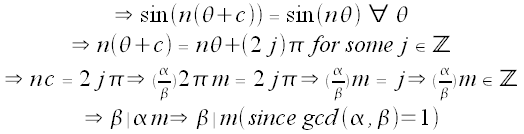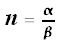The n-leaf Rose
|
|||||||||
|
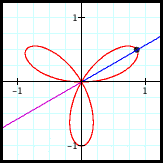
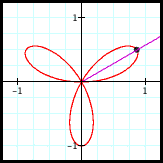
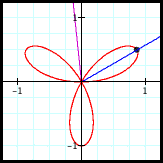
If a polar graph is cyclic, then its cycle c must be a multiple of π. Why is this? In the drawings below, the blue ray represents θ = θ0, and the purple ray represents θ = θ0 + c for some c. Any point with θ = θ0 + c must lie either on the purple ray (if r > 0) or on the opposite ray (if r < 0). Note that when c is not a multiple of π, the purple ray (and its opposite ray) intersect the blue ray (and its opposite ray) only at the origin. Thus, if the cycle c is not a multiple of π, then the point (θ0, r(θ0)) and (θ0 + c, r(θ0 + c)) cannot coincide unless the point lies at the origin.
And the point r(θ) cannot always be at the origin since sin(nθ) is not identically zero (we are assuming n ≠ 0). So c must be a multiple of π.
Furthermore, note that if c is an even multiple of π
And if c is an odd multiple of π
(The point must lie on the ray opposite the purple ray.)
If c = (2m)π, then
And if c = (2m + 1)π, then
So if the polar function r(θ) = sin(nθ) is cyclic,
That is, if n is irrational, the graph will never trace over itself,
Let What is the cycle of r = sin(nθ)? Let's find out!
We know c is either an even or odd multiple of π,
Try: c = (2m + 1)π for some integer m
Then we need
We want c to be as the minimum positive number such that
And by the above, the smallest positive value of j we can choose is α, so
So c = βπ. Note that, by (1), we must have that α and β are both odd. Otherwise, (1) gives a contradiction.
Try: c = (2m)π for some integer m
Then we need
We want c to be as the minimum positive number such that
And by the above, the smallest positive value of m we can choose is β, so c = 2mπ = 2βπ.
So if either α or β is even, we have
So, to summarize, we have found the following:
Now, using this information, we can quickly come to some conclusions about the number of "petals" on the "rose" formed by the equation
Click here to see that analysis.
|
 θ
θ
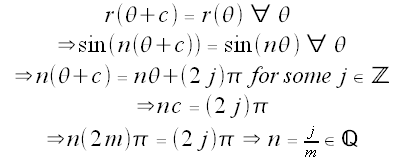
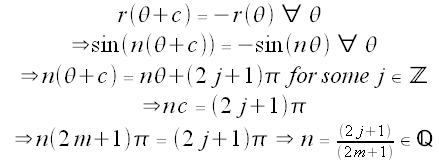
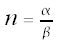 , where gcd(α, β) = 1.
, where gcd(α, β) = 1.