Note that the number of petals on the rose is equal to the number of times the graph passes through the origin in one cycle.
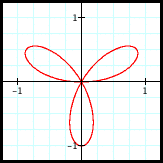
r = sin(3θ)
3 passes through
the origin,
3 petals
|
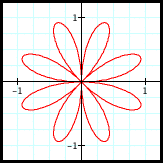
r = sin(4θ)
8 passes through
the origin,
8 petals
|
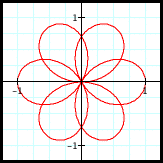
r = sin((3/2)θ)
6 passes through
the origin,
6 petals
|
How many times does the graph of r = sin(nθ)
pass through the origin in one cycle?
The graph passes through the origin whenever r = 0,
so we need to find the number of values of θ such that sin(nθ) = 0.
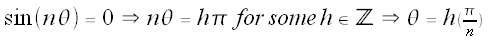
To count the number of multiples of 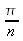 within the interval [0,c),
within the interval [0,c),
(and thus the number of petals)
we divide the cycle lengths c we found earlier by 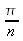 ,
,
and we find the following:
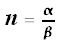 |
# of petals |
α and β both odd |
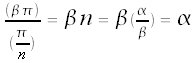 |
either α or β even |
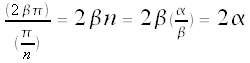 |
So the graph of 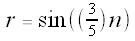 has 3 petals,
has 3 petals,
the graph of  also has 3 petals,
also has 3 petals,
the graph of 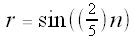 has 4 petals,
has 4 petals,
the graph of 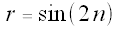 also has 4 petals,
also has 4 petals,
the graph of 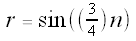 has 6 petals,
has 6 petals,
etc.
<< Previous (Cycles)
Return to my page
Return to EMAT 6680 page




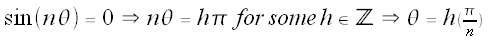
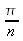 within the interval [0,c),
within the interval [0,c),
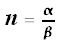
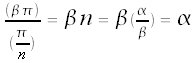
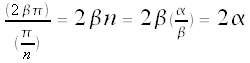
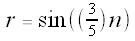 has 3 petals,
has 3 petals,
 also has 3 petals,
also has 3 petals,
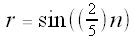 has 4 petals,
has 4 petals,
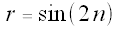 also has 4 petals,
also has 4 petals,
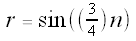 has 6 petals,
has 6 petals,