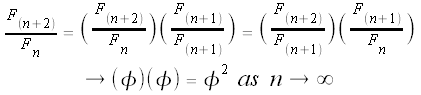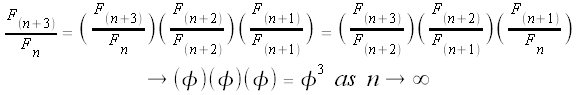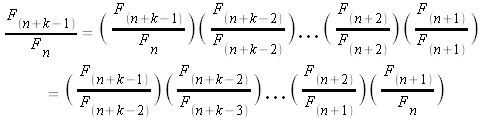φ and Fibonacci
|
|
Let's move on to a seemingly unrelated idea--the Fibonacci sequence.
F0 = 1, F1 = 1, and Fn = Fn-2 + Fn-1 for n ≥ 2. That is, the first and second (or "zeroth" and first) terms of the sequence are both 1, and each of the other terms is defined to be the sum of the two previous terms. So the first few terms of our sequence are
F0 = 1 Spreadsheets are a great way to investigate recursively-defined functions and sequences like this one, because one can define a certain cell in terms of other cells. Try creating a spreadsheet with the first 50 Fibonacci numbers in the leftmost column. You can type 1 into cells A1 and A2, then type =A1+A2 into cell A3, and copy and paste cell A3 into cells A4, A5, A6, ..., all the way to cell A50. See how easy that was? Here's what mine looks like. You can click on a cell and then look at the function bar at the top of the screen to see the formula used to calculate that cell.
Now, in the second column, use the formula capability again to calculate the ratio of consecutive Fibonacci numbers (with the later number on top; that is, make it
The ratio of consecutive Fibonacci numbers
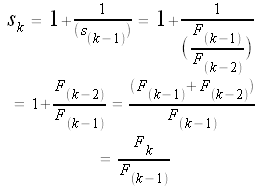
We have shown that
Dividing both sides by
We can replace the second
So
Again, we can replace the second
Repeating this process "forever," we get the continued fraction representation of
Let's use this fact to get better and better approximations of We can compute just part of this continued fraction, and as we compute longer and longer pieces, we'll get better and better approximations.
Let
Since these are increasingly long "pieces" of the continued fraction representation of Also note that
More generally,
Let's calculate some values of our si's:
Conjectures?
It looks like
Base case: n = 1
Induction hypothesis:
Induction step:
By hypothesis, we have
Thus, for all n ≥ 1, we have
And we have shown that sn approaches Q.E.D.
Now go back to your spreadsheet and add a few more columns:
Do you see any patterns? Look for functions of
It looks like the third column approaches Wow! Why is this? Let's find out!
We showed above that the ratio of consecutive Fibonacci numbers approaches
Third column:
Fourth column:
Now let's generalize this idea to the kth column
There are k-1 factors in this product,
We have shown that the values in the kth column (the ratio of every kth Fibonacci number) approaches
|
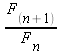 , not
, not 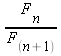 ). Make sure your cells show their value to several decimal places. Calculate the ratio many times for different pairs of consecutive Fibonacci numbers, until the ratio starts to "level off." Notice anything?
). Make sure your cells show their value to several decimal places. Calculate the ratio many times for different pairs of consecutive Fibonacci numbers, until the ratio starts to "level off." Notice anything? 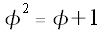 .
.
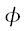 , we have
, we have 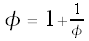
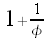
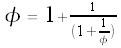
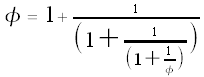
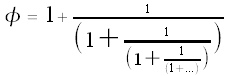
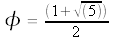 , but soon you'll see why these approximations will help us.)
, but soon you'll see why these approximations will help us.)
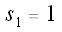 ,
, 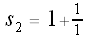 ,
, 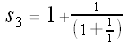 ,
, 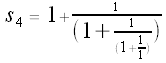 , etc.
, etc.
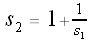 ,
, 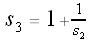 ,
, 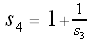 , etc.
, etc.
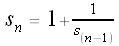
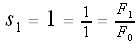
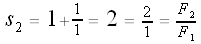
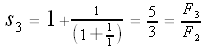
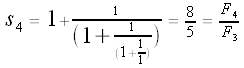
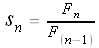 for all n ≥ 1.
for all n ≥ 1.
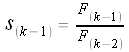
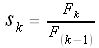 .
.
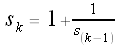
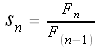
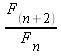 ); in the fourth column, every fourth Fibonacci number (
); in the fourth column, every fourth Fibonacci number (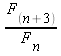 ); etc. Make as many columns as you like.
); etc. Make as many columns as you like.