In this lesson the students are drawing rotations of a triangle around a cirlce to find the rotation matrices.
Students can work in pairs if they choose. There are two parts to this activity.
PART 1:
1. Using the computer the students need to open the Geometer Sketchpad program and a new document.
2. Go to the menu and click on Graph. Highlight grid form and then choose square grid. (a grid should appear in the document)
3. Go to the menu again and click on Graph. This time go to plot points. Plot the origin and a grid point that is in the 1st quadrant.
4. Label the origin point, O, and the grid point, A. (Use the label tool in the side toolbar)
5. Select the origin point and point A. Click on Construct on the menu bar. Choose circle-by-center plus point. Now a circle with center at O and point A lying on the circle appears on the grid.
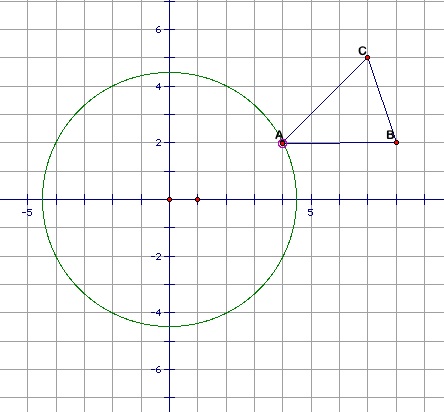
6. Go to the menu again and click on Graph. Go to plot points again, and this time we are going to plot two point that are in the 1st quadrant and lie outside of the circle.
7. Label these points B and C.
8. Connect points A, B, and C to form a triangle that looks something like this:

9. Select all the vertices and the sides of the triangle.
10. Go to the menu and click on Transform. Click on rotate. Plug 90 degrees in for the rotation and make sure it reads "about center O" before you rotate it.
11. Label this rotation with the corresponding vertices: A', B', and C'.
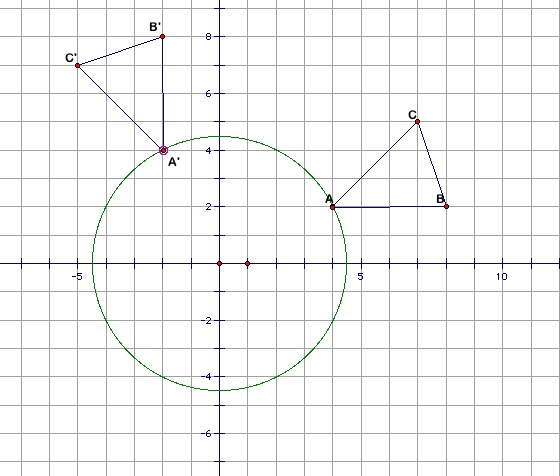
Q1: What are the coordinates of this new triangle A'B'C'? What relationship do you notice between the original triangle ABC and the rotated triangle A'B'C'? Explain.
12. Predict what the coordinates of another 90 degree rotation of the triangle A'B'C' would be around the origin.
13. Perform this rotation. Repeat steps 9 and 10 using the triangle A'B'C'. Label this new rotation triangle A"B"C".

Q2. Were your prediction coordinates the same as the picture? Why or why not?
14. Do one last 90 degree rotation of triangle A"B"C" around the origin. Label these vertices A'"B'"C'".
PART 2:
1. On a sheet of paper, place the coordinates of the original triangle in a 3X2 matrix. Call this matrix L.
For the example above, the coordinates were A=(4,2), B=(8,2), and C=(7,5) so our matrix L looks like this:
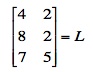
2. Now form the transformation matrix that will rotate our original triangle ABC to triangle A'B'C' and call this matrix T. (Remember what you discovered above and also the identity matrix.)
3. Do the matrix multiplication of matrix L by matrix T.
4. Compare the coordinates in this matrix with the coordinates of triangle A'B'C'. Was the hypothesis transformation matrix T correct? Why or why not?
5. Multiply the coordinates of triangle A'B'C' by your transformation matrix T.
6. How does this set of coordinates compare with the prediction in Part 1?
7. Again use matrix multiplication to multiply the coordinates of triangle A"B"C" by the transformation matrix T.
8. Determine the coordinates of triangle A'"B'"C'".
9. Make another comparison of the coordinates
found using the transformation matrix T and the coordinates you
found for triangle A'"B'"C'", are they the same?
If they are explain why and if they are not try to find the correct
transformation matrix that would give you the correct coordinates.
Click
Here for Homework Assignment