Claudette Tucker
Problem: Candy Problem
Daniel purchased a bundle of candy during three different weeks for three different amounts. We want to know the amount in dollars, X, that he or she would have to pay given that there is a one pound purchase of each candy, jelly beans, chocolates, caramels, licorice.
In order to determine the amount in dollars, X, for a pound of each candy, it suffices to develop a system of equations for DanielŐs candy purchases. So we have,
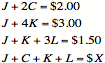
It seems as though one should be able to manipulate the
first three equations for substitutions in order to determine the values of J,
C, K, and L; however, this immobilized possible solutions. This immobilization led to another
strategy. The numbers 2, 4, and 3
have common multiples, such as 12, 24, and 48. For simplification purposes, it suffices to use the least
common multiple of 2, 3, and 4.
We want to manipulate the first three equations so that we have twelve
times each pound of candy, 
. If
we multiple the first equation by 6 and the third equation by 4, then we will
have the following system of equation.
Notice that this yielded 12C and 12L. Now, we must determine how one can
obtain 12J and 12K. Now, we must
manipulate the second equation in order to produce 12J and 12K. We want the following: 
and
. So, we must
multiply the second equation by two to achieve an equation where thereŐs twelve
times each pound of candy.
The sum of the system of equations is 
. Recall that we
want to determine price of all candies, x, given that Daniel purchases one
pound of each type. If we divide
both sides of the equation by twelve, then it yields that Daniels will pay
$2.00 for a pound of each candy.