The Vertex Question
Is it possible to construct the vertex of the graph of a parabola given only a finite number of points on the parabola's graph?
The students will likely approach this problem naively, i.e. trying to utilize algebra to determine the coordinates of the vertex and then merely plotting those coordinates. Remind them of the limitations of geometric construction. It may be helpful to remind them that a parabola has a geometric definition, as well as an algebraic. That is, it is precisely the set of points in the plane equidistant from a point (its vertex) and a line (its directrix). The following Java applet may allow them to see this: by moving any of the points (the focus, or either of the 2 highlighted points on the directrix) they can see that the parabola changes.
One key idea for the students to remember is that while a given point is the same distance from the vertex as it is from the directrix, this distance is different from point to point - see this sketch. Unfortunately, we do run into some technical issues when trying to use GSP to dynamically construct the vertex, namely that GSP cannot construct the intersection of a line and a locus of points (like a parabola). This means that our ability to use GSP for this proof is somewhat limited. Included below is a set of pictures designed to show how one possible proof might go. Now, it is possible to 'trick' GSP into plotting the vertex, but it's not done strictly as a construction. This can still prove useful, however, as it will allow us to view the locus of points created by varying the parameter b. An example is given here.
Suppose we have the parabola below with three points identified as A, B, and C.
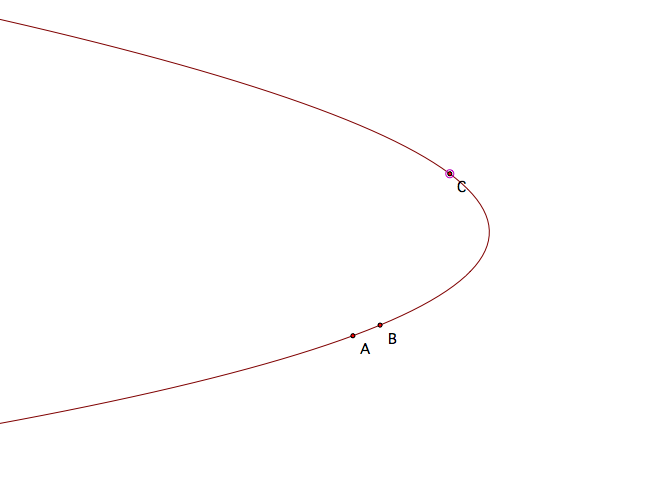
Construct the line segment from point B to point C, and construct the line parallel to this segment through A.
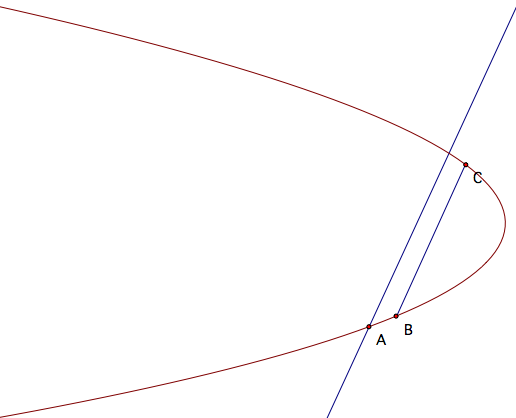
Now, find the midpoint of the segment from A to the intersection of this line with the parabola, call it D (this is where things start to get fouled up in GSP). Then, the line through the midpoints of the segments AD and BC will be perpendicular to our directrix, so construct this line also.
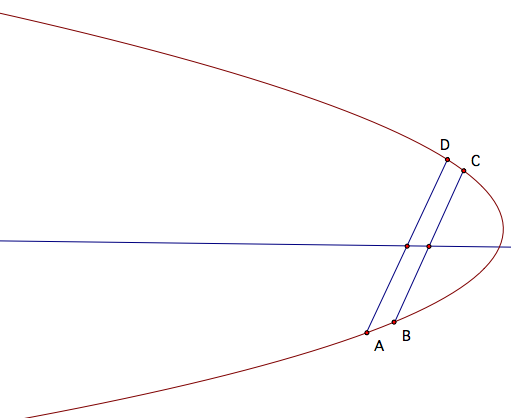
Now, take any point on this new line and construct a perpendicular through it. This new chord is parallel to the directrix and its midpoint lies on the axis of symmetry of the parabola.
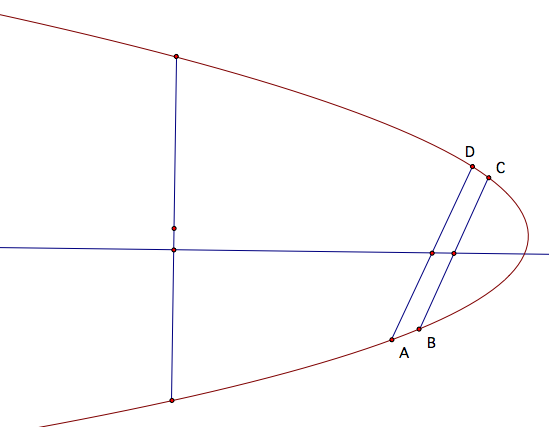
Thus, we can construct a perpendicular through its midpoint and voila! we have the vertex of the parabola.
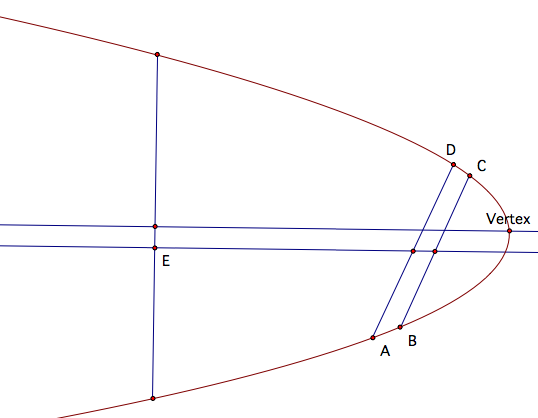
Now, one minor and yet very interesting little aside is available to your students: We just constructed the vertex of the parabola using 3 points. Will any 3 points work? What if the vertex is not visible, much less identified? i.e. What if you only have this part of the parabola:
Whether or not one pursues this avenue of exploration is heavily dependent on the aptitudes and desires of one's students. For a detailed look, see the nice article in Mathematics Magazine, Vol. 51, No. 5, (Nov. 1978), pp. 294-298, by Leon Henkin and William A. Leonard.
Another interesting idea lends itself to further consideration, however. Many students will assume that, if they are given a parabola, they are also given the focus and/or directrix. A natural extension of this problem is to ask if constructing the vertex is equivalent to constructing the focus, or the directrix? An outline may be found here.