Transformations of the Sine and Cosine Graph – An Exploration

By Sharon K. O’Kelley

This is an exploration for Advanced Algebra or Precalculus teachers who have introduced their students to the basic sine and cosine graphs and now want their students to explore how changes to the equations affect the graphs. This is an introductory lesson whose purpose is to connect the language of Algebraic transformations to the more advanced topic of trignonometry. (A key follows the end of the exploration.)

1. Consider the basic sine equation and graph. Let’s call it the first function….

2. If the first function is rewritten as….

then the values of a = 1, b = 1, and c = 0.

Let’s find out what happens when those values change….

3. Take a look at the blue and red graph and their equations. The graph of the first function remains in black.

Equation of blue graph

Equation of red graph

a. Describe how the equation of the first function has changed to become the equation of the graphs in blue and red. This value is called the amplitude of the graph.

b. Describe how the graph of the first function has changed to become the blue graph and the red graph. Be as specific as possible. Include in your answer how a specific point on the graph of the first function transforms to become a point on the blue graph and on the red graph.

c. Take a look at an animation of this phenomenon. Click here…. (Be patient. These movies take awhile to load….)

4. Now consider the purple and green graph and their equations. The graph of the first function remains in black.

Equation of purple graph

Equation of green graph

a. Describe how the equation of the first function has changed to become the equation of the graphs in purple and green.

b. Describe how the graph of the first function has changed to become the purple graph and the green graph. Be as specific as possible. Include in your answer how a specific point on the graph of the first function transforms to become a point on the purple graph and on the green graph.

c. How does “b” operate differently from “a” in the equation? Look deeper than horizontal versus vertical….

d. Take a look at this phenomenon…. Click here….

5. Examine the purple and green graph and their equations. The graph of the first function remains in black.

Equation of red graph

Equation of green graph

a. Describe how the equation of the first function has changed to become the equation of the graphs in purple and green.

b. Describe how the graph of the first function has changed to become the red graph and the green graph. Be as specific as possible. Include in your answer how a specific point on the graph of the first function transforms to become a point on the purple graph and on the green graph.

c. See how it moves…. Click here….

6. Consider the blue and purple graph and their equations. The graph of the first function remains in black. This value is called the phase shift of the graph.

Equation of blue graph

Equation of purple graph

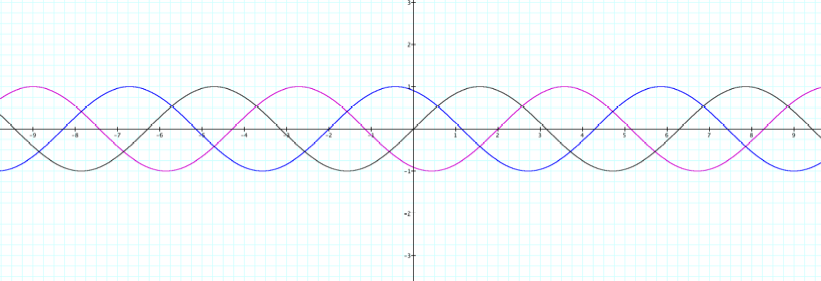
a. Describe how the equation of the first function has changed to become the equation of the graphs in blue and purple.

b. Describe how the graph of the first function has changed to become the blue graph and the purple graph. Be as specific as possible. Include in your answer how a specific point on the graph of the first function transforms to become a point on the blue graph and on the purple graph.

c. How does “c” operate differently when it is inside or outside the parentheses? Look deeper than horizontal versus vertical….

d. Take a look…. Click here….

7. What about negatives?

a. Examine the following graphs…. (The first function is in black.)

Equation of red graph

Equation of blue graph

b. Compare the graphs. Describe in detail the transformations you see.

8. Throwing it all together….

Consider the graph of ….

(The first function is in black.)

Describe the transformations fully. Be as specific as possible.

(Hint: Look at this problem as .)

9. The Cosine Graph

a. On a sheet of graph paper, predict what the following graphs would look like.

10. Let’s go a little further…. Write two different equations for the same graph below. Use sine in one and cosine in the other. Verify your answer with graphing software or a graphing calculator.

11. Summarize what you have learned here. Use definitions and examples. Be specific.

Key to the Exploration

3. a. The value of “a” is 2 and .

b. The blue graph is stretched vertically by a factor of 2. This can be determined by comparing point (1.57, 1) on the first function to point (1.57, 2) on the blue graph. The red graph is shrunk vertically by a factor of . This can be determined by comparing point (1.57, 1) on the first function to point (1.57, ) on the

red graph.

4. a. The value of “b” is 2 and .

b. The purple graph is shrunk horizontally by a factor of . This can be determined by comparing point (1.57, 1) on the first function to point (0.785, 1) on the purple graph. The green graph is stretched horizontally by a factor of 2. This can be determined by comparing point (1.57, 1) on the first function to point (3.14,1) on the green graph.

c. The values for “a” and “b” seem to be inverted. In other words when “a” is it is a vertical shrink by . When “b” is , however, it is a horizontal stretch by a factor of 2. This can easily be explained by the fact that you are solving, so to speak, for the given variable. For example, is equivalent to ; therefore, when the variable is isolated it seems straightforward. However, the x isn’t isolated in these cases….

5. a. The value of “c” is 2 and .

b. The red graph is translated up by 2 units. This can be determined by comparing point (0,0) on the first function to point (0, 2) on the red graph. The green graph is translated down by 2 units. This can be determined by comparing point (0, 0) on the first function to point (0, ) on the green graph.)

6. a. The value of “c” is 2 and .

b. The blue graph is translated left 2 units. This can be determined by comparing point (0,0) on the first function to point on the blue graph. The purple graph is translated right 2 units. This can be determined by comparing point (0, 0) on the first function to point (2,0) on the purple graph.

c. Outside the parentheses, positive c is up and negative c is down. Inside, it seems opposite than what you would assume. Positive c is to the left and negative c is to the right.

7. They look the same! Why? Because sine is a periodic function, a vertical reflection and horizontal reflection yield the same image.

8. The graph has translated right units. It has been horizontally shrunk by a factor of and vertically shrunk by a factor of .

9. * (red)

* (blue)

* (purple)

* (green)

* (yellow)

10. Possible answer: and

11. Students’ answers should cover definitions and descriptions of the transformations as well as how the generic equation changes. They also should define “amplitude” and and “phase shift.”

Return