Parametric Curves and Trigonometry

By Sharon K. O’Kelley

Introduction

Consider the equations…

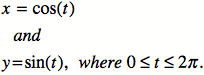
Notice that squaring both equations yields…

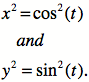
Using the Pythagorean Trigonometric Identity, we know that…

Using substitution, it can be established that…

which is the equation for the Unit Circle.

The parameter of t, therefore, can be viewed as the angle of rotation as the terminal ray containing point (x, y) moves counterclockwise around the unit circle. (See figure 1.). The ordered pair (x,y) can also be regarded as (cos(t), sin(t)).

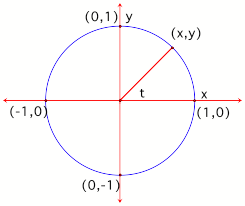
Figure 1

Varying “a” and/or “b”

What happens if a and/or b are varied in the following equations?

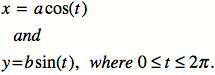
Let’s experiment. What if “a” is two and “b” is one? This would yield the following values….

t (degrees)	t (radians)	x	y
		2	0
		0	1
		-2	0
		0	-1

If these equations were graphed, it would look like the following….

(Note that if “a” were negative, it would still yield the same graph because the values would switch – e.g. t = 0 would yield (-2,0) and t=180 would yield (2,0)).

Notice that this yields a horizontally-oriented ellipse whose major axis has a measure of 4 units and whose minor axis has a measure of 2 units. In essence, the unit circle has been horizontally dilated by a factor of 2 to yield the ellipse.

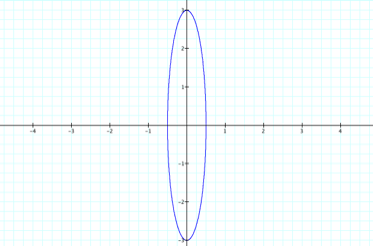
What if the following equations were given?

A prediction can be made that a graph of these equations would be a vertically-oriented ellipse with points (1/2, 0), (-1/2,0), (0, 3) and (0,-3).

Return