
An Introduction to Tangent Circles
By Sharon K. OŐKelley
1. Consider this problemÉ. Using
GeometerŐs Sketchpad, find the two lines tangent to a circle from an external
point.
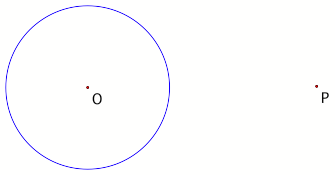
Figure 1
a. To solve this problem, a student must
understand the concept of tangent. A line is tangent to a circle when it
intersects the circle in one point. At that point, the radius of the circle forms
a right angle with the tangent line. If the radius forms a right angle with the
tangent line, then the segment OP becomes the hypotenuse of the right triangle.
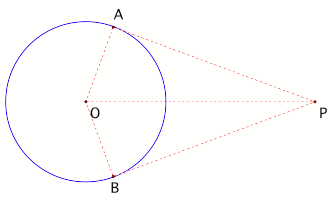
Figure 2
b. Since an inscribed angle is
one-half the measure of the arc it subtends, OP must be 180 degrees since angle
OAP is a right angle. Therefore segment OP is the diameter of a second circle
that passes through the points of tangency. Using the midpoint of OP as its
center, a circle is constructed with a radius of one-half the measure of
segment OP. Where this circle intersects the first circle are the points of
tangency. These points can now be connected to point P thus forming the tangent
lines.
Solution

Figure 3
2. What about finding
tangent circles? ConsiderÉ.
Given a line and a
circle with center K. Take an arbitrary point P on the circle. Construct two
circles tangent to the given circle at P and tangent to the line.
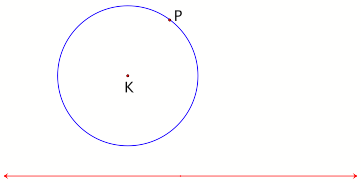
Figure 4
a. First, a right angle must be constructed through point P with the
radius of circle K to create the point of tangency.
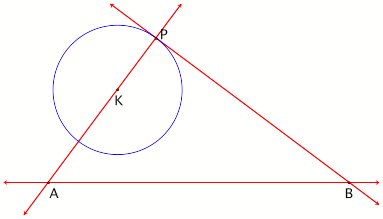
Figure 5
b. One tangent circle can
easily be constructed using the midpoint of segment KP as its center.
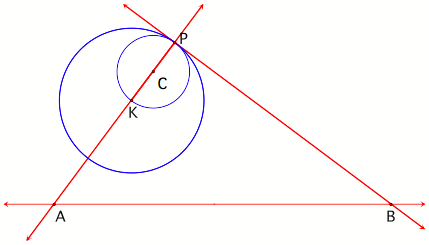
Figure 6
c. The second tangent
circle can be found on the other side of line PB.
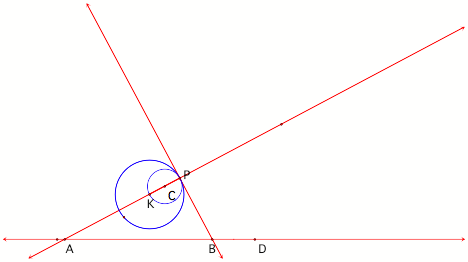
Figure 7
d. Keep in mind that in order for the second circle
to be tangent to line AB as well as to Circle K at point P, its center must be
equidistant from the sides of angle PBD. Therefore, its center must fall on the
angle bisector of angle PBD.
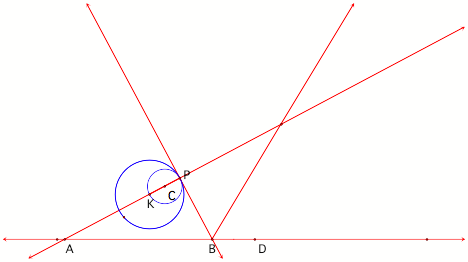
Figure 8
e. Now the second tangent circle can be
constructed using the intersection of line AP with the angle bisector as its
center.
Solution:

Figure 9
3. What about circles that
are tangent to only circles as seen in Figure 11? How are these created? How
are they related to the construction of an ellipse or a hyperbola? For a
discussion of the relationship between conics and tangent circles, go here to see a GeometerŐs Sketchpad presentation of
the topic.
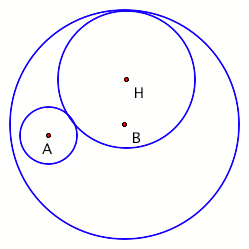
Figure 10