
The Final
by Sharon K. O’Kelley
Part One – Bouncing
Barney
Barney
is in the triangular room ABC. He walks from a point on BC parallel to AC. When
he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns
and walks parallel to AB. Prove that Barney will eventually return to his
starting point. How many times will Barney reach a wall before returning to his
starting point? Explore and discuss for various starting points on line BC,
including points exterior to segment BC. Discuss and prove any mathematical
conjectures you find in the situation.
Discussion
1. To
explore this phenomenon, I decided to look at the specific situation in which
Barney (indicated by point D in figure 1) starts at the midpoint of side BC.

Figure 1
Notice
that by constructing the parallel lines as called for in the directions, Barney
ends up where he started at point D after touching each side once. Therefore,
it can be said that Barney made one circuit around the inside of the triangle.
The
Triangle Proportionality Theorem states if a line intersects two sides of a
triangle and is parallel to the third side then it divides the two sides into
segments of proportional lengths. Therefore, since D is the midpoint of side BC
and segment ED is parallel to AC, then E must be the midpoint of AB as well.
The same reasoning can be applied to find that F is the midpoint of AC.
Segments DE, EF and FD can then be called the midsegments of triangle ABC.
According to the Triangle Midsegment Theorem, when a midsegment of a triangle
is parallel to the third side of the triangle, its measure is one-half the
measure of the third side. Therefore, the measure of DE is one-half the measure
of side AC, the measure of DF is one-half the measure of side AB, and EF is
one-half the measure of side BC. The perimeter of triangle EFD (or Barney’s
circuit) is thus one-half the perimeter of triangle ABC.
2. What if Barney started at a point that
marked one-fourth the length of side BC as shown in figure 2?
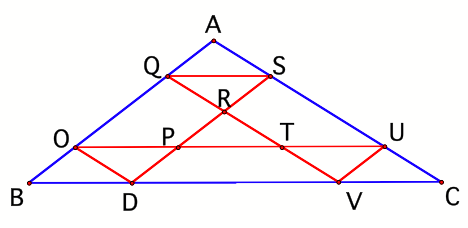
Figure 2
Following
the given directions in constructing parallel lines, Barney returned to point D
after touching each wall twice. What else can we discover?
We
know that segment BD is one-fourth the measure of segment BC, and by
construction, we know that segment OD is parallel to segment AC. Using the
Triangle Proportionality Theorem, we can state that since OD cuts off segment
BD which is one-fourth of segment BC, then BO is also one-fourth of segment AB.
The same reasoning can be applied around the triangle. If AQ and OB are each
one-fourth of side AB, then AQ is one-third the length of segment AO. Since
parallel lines have been constructed, it can also be concluded that triangles
AQS and AOU are similar by the Angle-Angle Theorem of Similarity. (Angle A is
congruent to Angle A and angles AQS and AOU are congruent because they are
corresponding angles of parallel lines.) Because these two triangles are
similar, their corresponding sides are proportional. Therefore, the length of
QS must also be one-third the length of side OU. This relationship holds for UV
and OD and their counterparts as well. We can also use the Angle-Angle Theorem
of Similarity to state that triangles AQS and ABC are similar with the measure
of QS being one-fourth the measure of side BC. This relationship holds around
the triangle as well. Thus the following can be concluded….
QS +OU = BC.
OD + QV = AC.
UV + DS = AB.
Therefore, QS + OU + OD + QV + UV + DS = BC + AC + AB.
Hence, the perimeter of
Barney’s circuit in this case equals the perimeter of triangle ABC.
3.
What if Barney started at a random point on segment BC?
From
the explorations above, I can deduce that Barney will always make it back to
his starting point, no matter where he starts, because of the Triangle
Proportionality Theorem. In this situation, the parallel segments are always
marking off proportional distances that relate each side to another side; therefore,
all the sides are interconnected proportionally through the parallel lines.
Thus the distances that are cut off by the parallel lines have to be the same
for all three sides which means Barney will eventually end up where he started.
Barney will also at most touch a wall two times. Combine the proportionality
theorem with the similar triangles created by the parallel lines as
demonstrated above and the conclusion can be drawn that the perimeter of
Barney’s circuit will always equal the perimeter of the triangular room except
in instances where Barney starts at the midpoint of one wall. Consider figure
3.
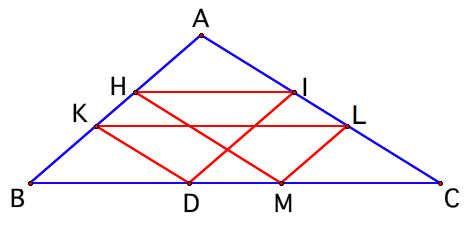
Figure 3
In figure 3, Barney’s starting
point at D has been randomly placed. Explorations with Geometer’s Sketchpad
reveal that he ends back up at point D after touching each wall twice and that
the perimeter of his circuit is equal to the perimeter of triangle ABC.
To see a GSP animation of this
situation, go here.
4.
What if Barney starts on a point outside of triangle ABC? Consider figure 4.
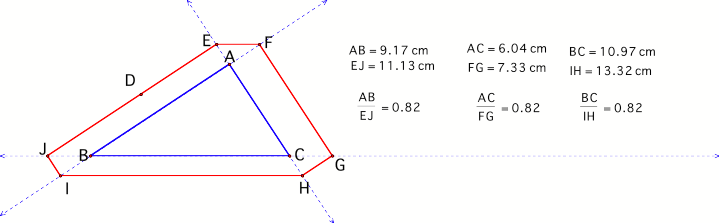
Figure 4
Notice
that when Barney starts outside the triangle at point D, his circuit goes
around the outside of the triangle. What is interesting to note is that no
matter how far Barney is from a wall when he starts the circuit, the ratios
between the sides of the initial triangle to the long sides of the circuit
parallel to those sides are constant as demonstrated in the figure above.
For
Part Two – Ceva’s Theorem, go here.