

Problems and explorations with second degree equations
by
Hyeshin Choi
3. What happens to y=ax^2+bx+c
(i.e., the case where b=1 and c=2) as a is varied? Is there a common point to all graphs? What is it? What is the significance of the graph where a = 0? Do similar interpretations for other sets of graphs. How does the shape change? How does the position change?
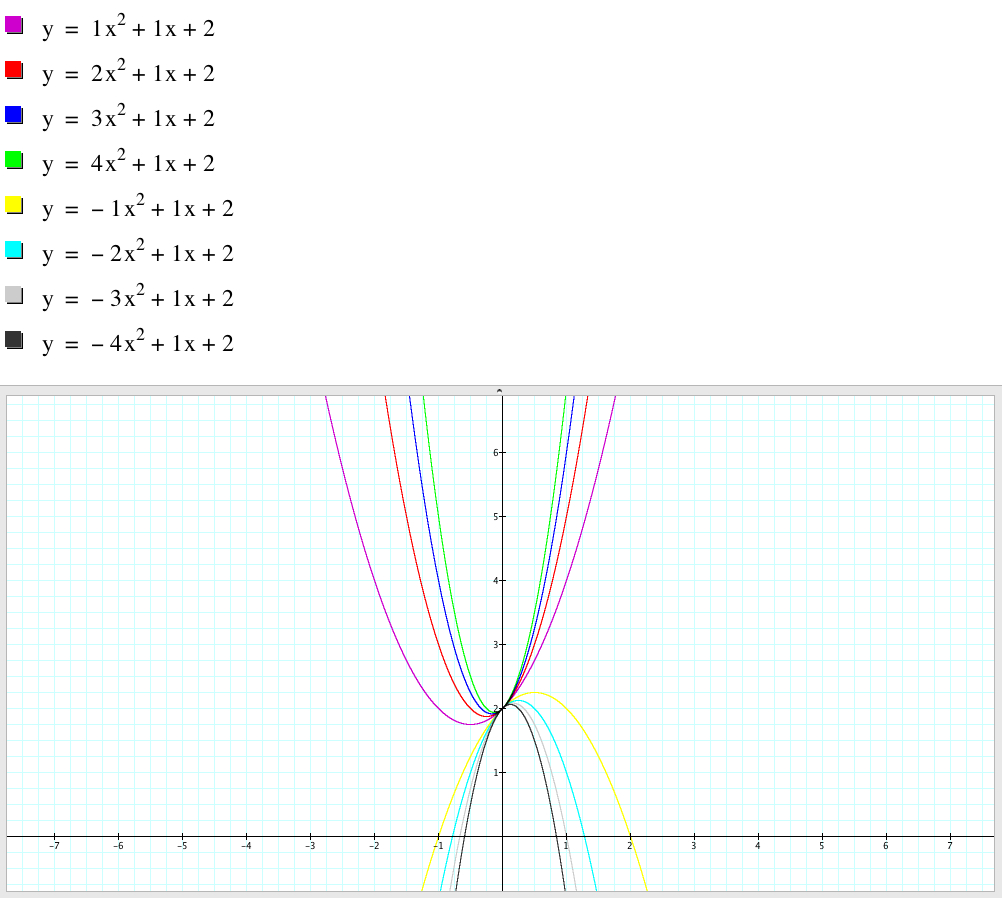
First I fix b=1 and c=2 and try a=from -4 to +4. Then the parabola opens upward when a is positive and it open downward when a is negative.
Also as a gets bigger and bigger the parabola shrink vertically which means that the parabola gets closer to x-axis.
Since I fixed c=2 which is the y-intercept when x=0. It can be expressed equation y=ax^2+bx is shifted 2 units up.
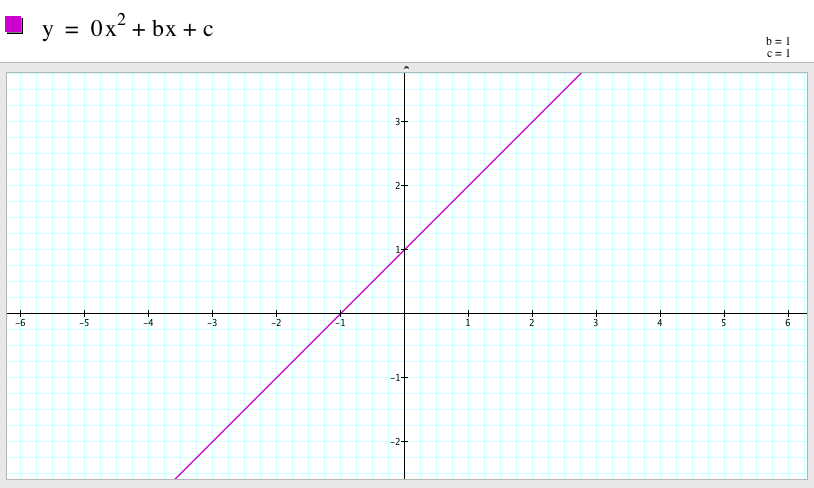
Let's see how does it lok like when a=0 (where b= and c=2). When a=0, the highest degree is 1 which is a linear equation.
Now let's try y=ax^2+3x-4.
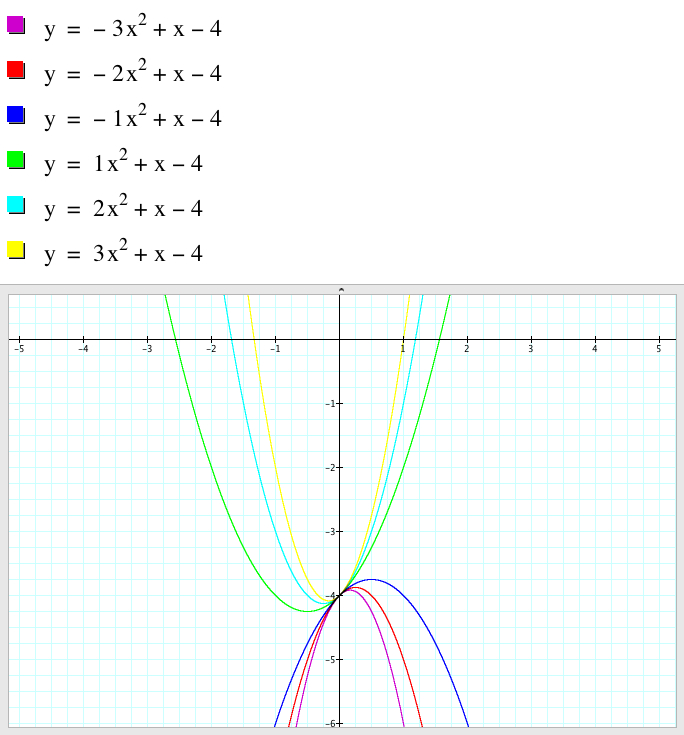
Since I change a=1 and c=-4, the common point of all graph is changed into -4.
The shape does not changed but is to shift to down 4 units from the origin.