
Assignment 3:
Quadratics in the XB Plane
by Bennett Lewis
In this assignment we will examine quadratics represented in the XB Plane and what it tells us about the graph. Before we jump into the XB plane, let's first revisit the equation
![]() .
.
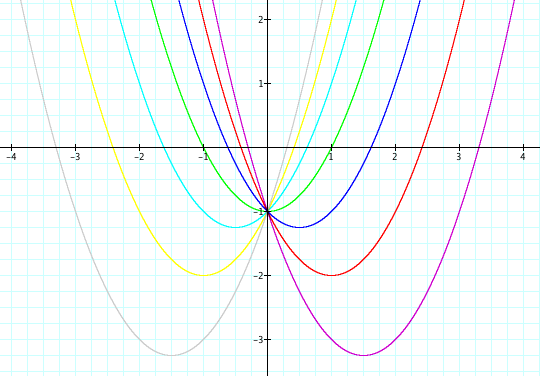
What would happen if we fixed a=c=1 and varied b? Let's take a look.
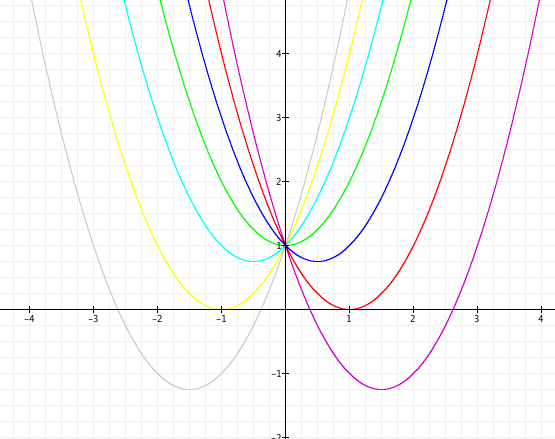
What can we observe from this graph? Well, first we can notice that when b=±3 that the graph has 2 real roots. When b=±2, the graph has 1 real root and lies tangent to the x-axis. When b = ±1 or b=0, the curve does not intersect the x-axis and thus has no real roots, but has complex roots. We can also notice that all the curves intersect the y-axis and each other at the point (0,1).
So then, how can we find the vertex of each curve? Well, from Assignment 2, we know a form of an equation that will show us the vertex. By completing the square we can get our equation into this form.
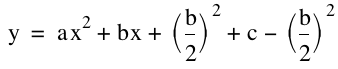
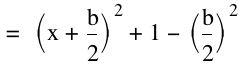
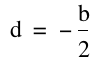 and
and 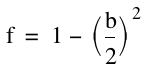
If we vary b in this form and overlay it onto the previous graph, we can see how the vertex intersects all of the vertices of the existing curves.
Check out the video of it here.
Now let's look at our original equation in the XB plane. To graph this, let b=y in a graphing application.
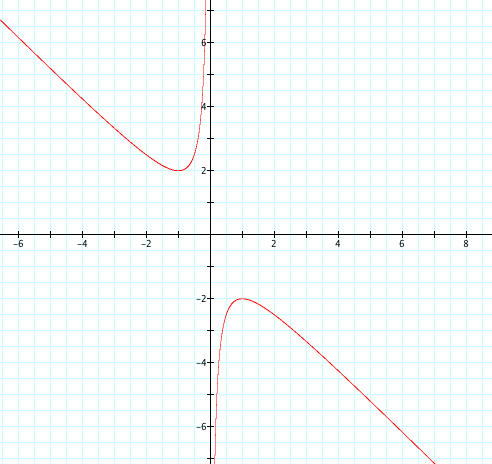
Notice the gap in the graph between -2 ≤ x ≤ 2. Remember what we found for roots between -2 and 2. Let's look at the same graph with -4 ≤ b ≤ 4.
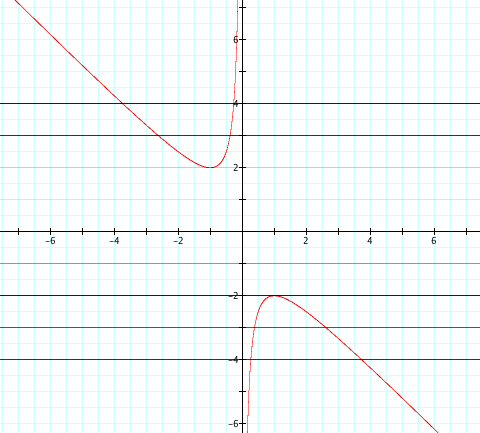
Notice how the lines b= -4, -3, 3, 4 intersect the curve twice. In our earlier investigation, we found that b = ± 3 had two real roots. Now lets look at b= ±2. These lines lie tangent to the curves and only intersect once, respectively. We found this to be true in our earlier case, that the quadratic equations only had one real root. Finally, let's investigate the gap in the middle. Notice, b= 1. This line does not intersect the curve. We found earlier that the quadratic equation had no real roots. Notice the same is true for values -2 < x < 2.
We have just established a relationship between the xb-plane and finding roots. Let's take a different value of c and see how it changes our graph in the xb-plane and what happens with the roots of that equation.
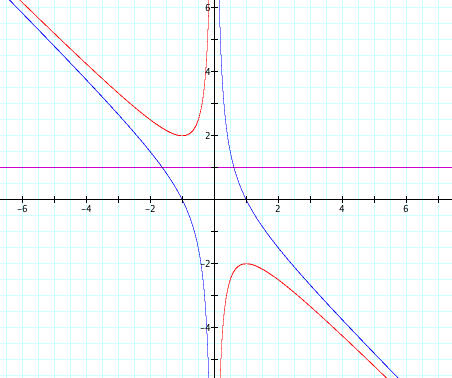
Notice that when c = -1, which is the case for the blue curve, there is no gap. From the relationship that we discovered this means that the equations has two real roots for all values of b.
Let's look at the quadratic equations of this curve as c = -1 and b is varied. Notice that there are always 2 real roots no matter the value of b.
Check out what happens as we vary c in this video here.
What happens when c = 0? Let's look at the graph.
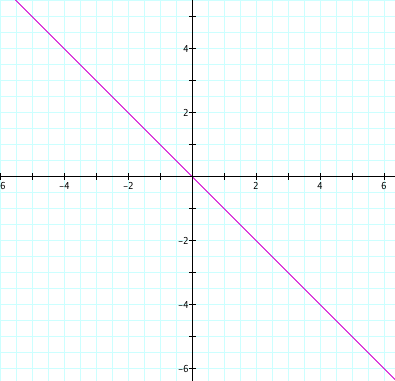
For this case, the curve intersects b values exactly once. Therefore for each value of b, there would be one real root for the quadratic equation.