Final Assignment
Part 3
Select one additional item from the assignments or from explorations presented in class that you have not written up. Submit a write-up about it.
The exploration I will write about is from Assignment 12 using Excel spreadsheets. Here is the problem I have chosen to look at:
6. Explore problems of maximization such as the lidless box formed from a 5x8 sheet with a square removed from each corner.
During the short time I have been at the University of Georgia, I have tutored student-athletes in several different math courses. One course is called Math Modeling (MATH 1101). This problem is similar to one that is used in this course. Some of the students I tutored struggled with this problem so I chose this problem in an effort create a page that I can use in the future to help students with this problem.
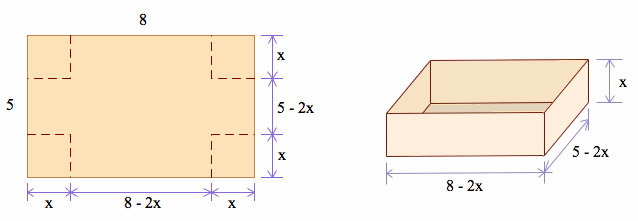
Suppose we have a piece of cardboard whose side lengths are 5 and 8. We want to make this piece of cardboard into a lidless box but to do so we have to cut out a square from each corner.
What size square can we cut out to maximize the volume of our box?
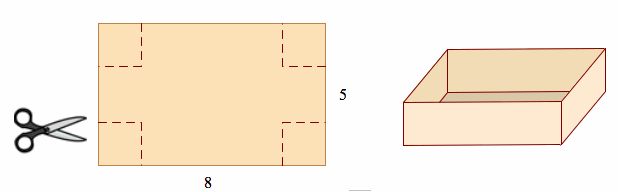
After we have cut out a square from each side, our cardboard rectangle will have the dimensions of
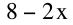and 
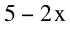. Since we cut out a length of x, the height for our new box will be x. Using the formula for volume we can substitute in our side lengths to get:
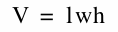
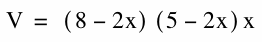
Now we can use Excel to find the maximum volume.
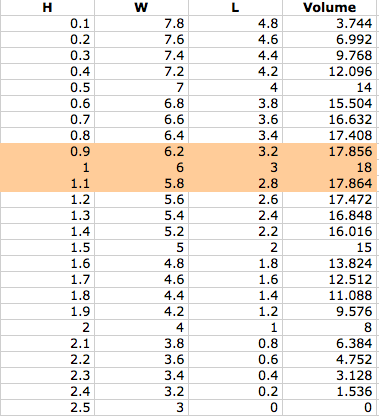
The smallest length we will consider is .1 and we will increase by .1 until we have reach 2.5. We will stop at 2.5 at because anything length bigger than this will be trying to cut out more cardboard than we actually have. The first column is the value of x, the second is the width (which we will say is 8-2x), the third is the length (which we will say is 5-2x) and the last column is the volume.
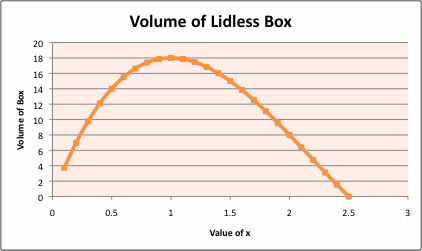
Here is the volume of the box graphed a function of the length of x:
Click here for the Excel file with this data and chart.
As we can see from the table and the graph, the maximum volume that can be achieved is 18 units.
We would have to cut a square whose side length is 1 to have the maximum volume of 18.