
In the previous investigation we looked at finding the tangent lines to two given circles. Now we are going to add onto that concept. In this investigation we are going to look at circles that are tangent to two given circles. Unlike the tangent lines investigation, we are going to look deeper than the construction of the tangent circles to try to understand their behavior and characteristics.

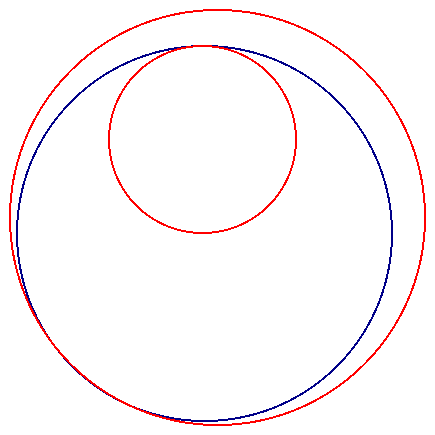
Similarly to when we constructed the tangent lines to two given circles there are several cases for us to consider with this problem. Each case is determined by where the two given circles lay with respect to one another. But within each case there are two types of tangent circles: one in which the tangent circle is in essence exterior to the one of the circles and another where the tangent circle engulfs more circles than the other tangent circle. Let's observe how each of the cases looks. There is when the circles do not intersect at all and one circle is completely contained in the second circle:

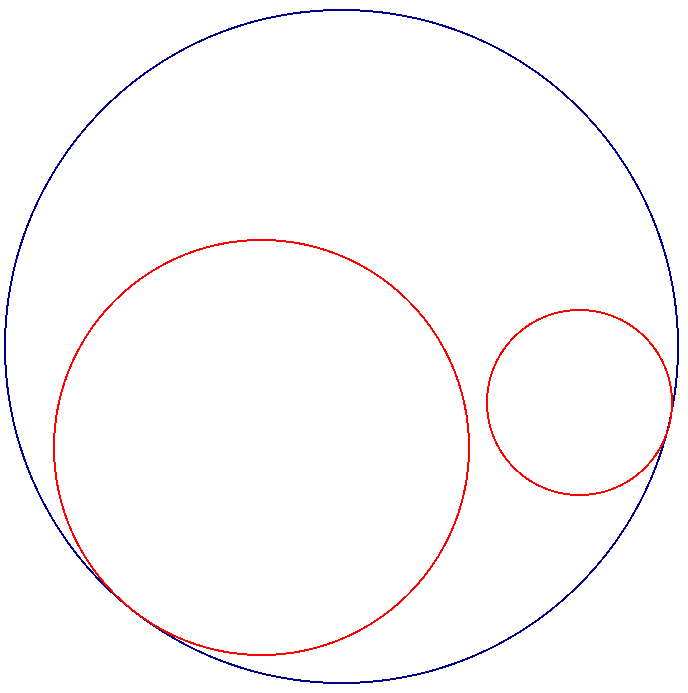
The next is where the circles still do not intersect but neither circle in contained in the other circle:

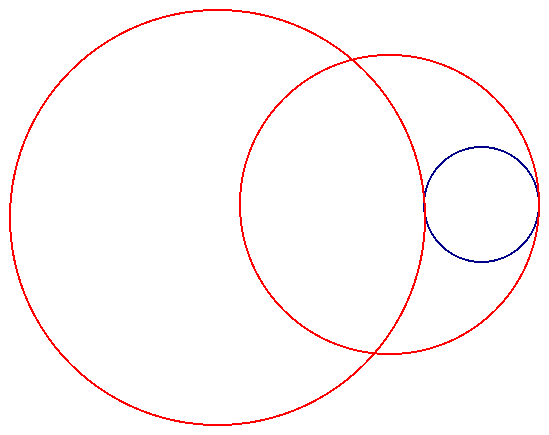
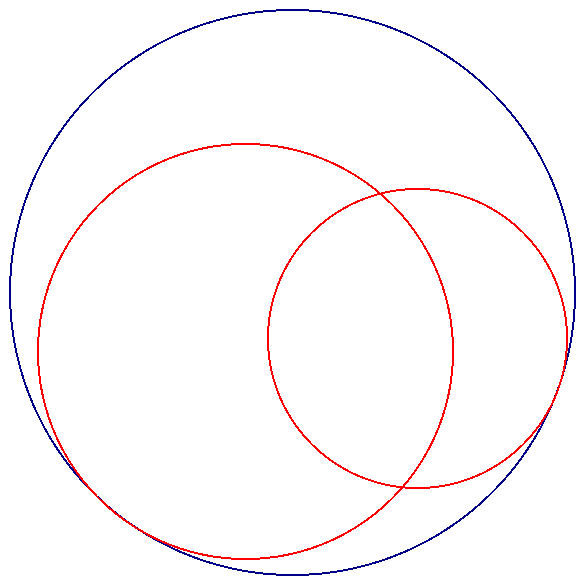
The final case is when the two circles intersect at two points:
Although we have several cases listed all of the first tangent circles were done using one construction and all of the second tangent circles were done using another construction. We did not have to use different tools for each cases in the way we did for the tangent lines investigation. Go here to try and do these constructions yourself. In order to know how these circles are constructed you can either use what you learned in the tangent lines investigation or use the tools for constructing tangent circles and use the "show script view" option to try and understand how the construction is done. The other way is to go to this page and construct the circle using the instructions given. While you are in Geometry Sketchpad play with these tangent circles. On the page there is only example of each type of tangent circle for each case. Are there others? What happens when you move the circles around or change their sizes? What happens when you move the point of tangency. Does it make a difference on which circle the point of tangency lies? Feel free to use such tools as trace and animate to explore these questions.
Now that we have constructed the circle tangent to two given circles and have an intuition to how those tangent circles behave let's look at the mathematics behind these characteristics. There is a common theme in math that is "you shouldn't think something, you should know it". That means that although exploration is important, it is not enough to stop there. We should try to prove our conjectures using definitions and geometric tools. What we are going to explore right now is when given a pair of circles how does the center of our tangent circle move? It should be clear that once the center of a tangent circle is found the circle itself is defined because only one circle centered at a set point with be tangent to two given circles. Therefore, we are going to explore the loci of the centers of our tangent circles and find out why they trace out the shapes that they do.
Start with the first case: two circles that do not intersect and one is completely contained in the other.
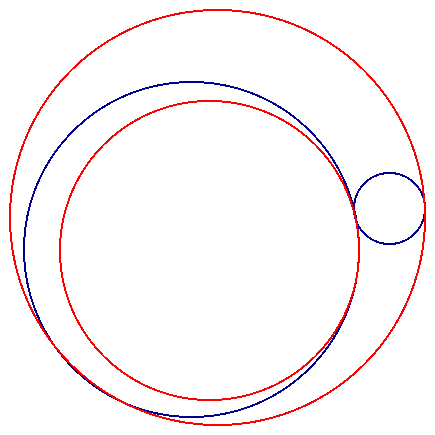
When we trace out the centers of the two tangent circles (green) we get what appears to be ellipses.

The picture is getting a little crowded so we are going to look at one tangent circle the locus of its center at a time. The given circles are centered at A and B. At this point it is assumed that the construction of this circle is understood.
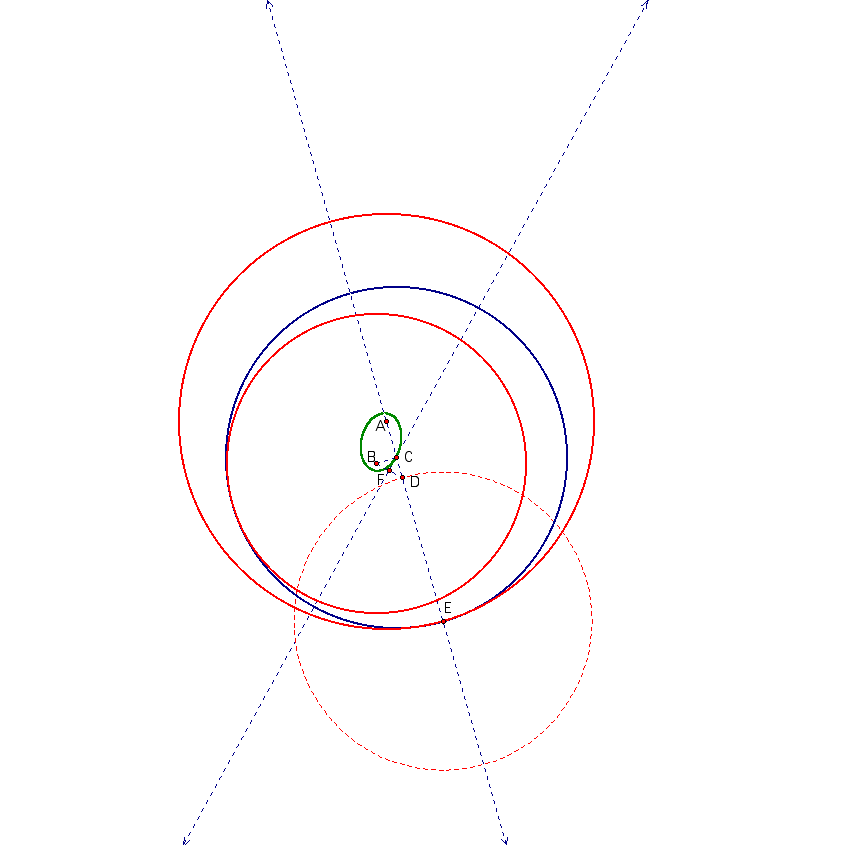
Things that are important to notice about this picture are: the line on which C and F lie is the perpendicular bisector of segment BD and that makes the triangle BCD an isosceles and that AE and DE are constant distances because they are radii of circles. We are conjecturing that the green locus is an ellipse with foci A and B. The definition of an ellipse is the set of points such that the sum of their distances from the foci are constant. In order to show that the green trace is an ellipse we need to show that AC+BC is a constant number. Since BCD is an isosceles triangle then BC=CD. Now we see that
Notice that since A, C, D and E are colinear AC+CD+DE=AE and now we see that
But here is the kicker, we already stated that AE and DE represent the radii of circles are therefore are constant. That means that their difference is a constant as well. Since AE-DE is constant then AC+BC is constant as well. Now we know that the locus of the center of this tangent circle is an ellipse with the centers of the two given circles being its foci.
For the other tangent circle in the same case the arguement is almost identical. Now the progression goes
AC+BC=AC+CD
AC+CD=AE+ED and so AE+BC=AE+ED
Since AE+ED are radii AE+ED is constant and so AC+BC is constant and again our trace is an ellipse with A and B the foci.
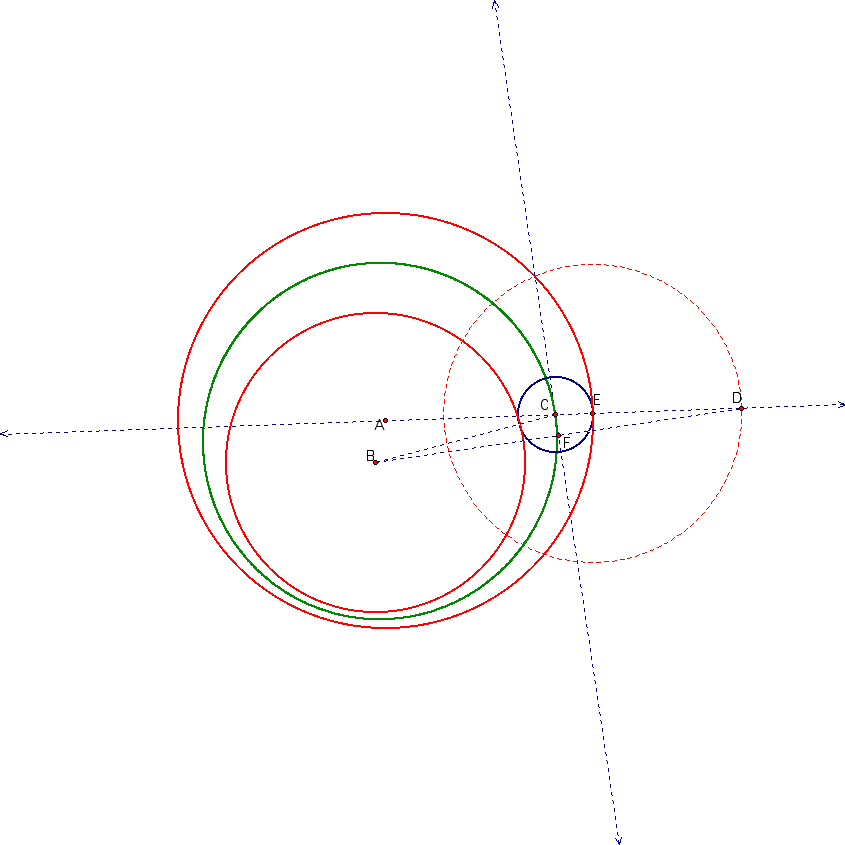
Now let's observe what we get when we look at the case of the two given circles being disjoint but one is not contained in the other.

When we trace the centers of the constructed tangent circles it looks like this
Both of the loci of the centers appear to be hyperbolas. We are going to look at the proof to show that indeed the locus of the center of one of the constructed tangent circles is a hyperbola. Showing it for the second constructed tangent circle will be an exercises left to the reader. Like in the last case the first thing we will do is look at the lines used in constructing this circle.
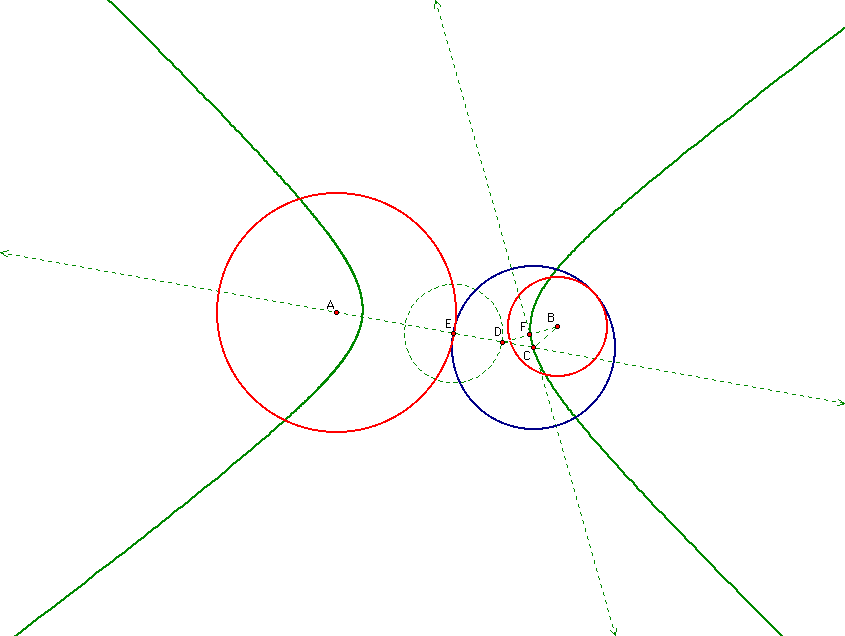
Some important things to notice about this picture are that CD=CB since DCB is an isosceles triangle, AE and ED are both constant values because they represent radii of circles, and that AE+ED+DC=AC since A, E, D and C are colinear. The definition of a hyperbola is the locus of points such that the difference of the distances from each of those points to the foci are constant. I claim that A and B are the foci of this hyperbola. Therefore my goal is to show that AC-BC is a constant value. We already stated that BC=CD which means
We also stated that AC=AE+ED+CD which leads us to
Since AE and ED are constant values then their sums are also constant. That gives us what we want because
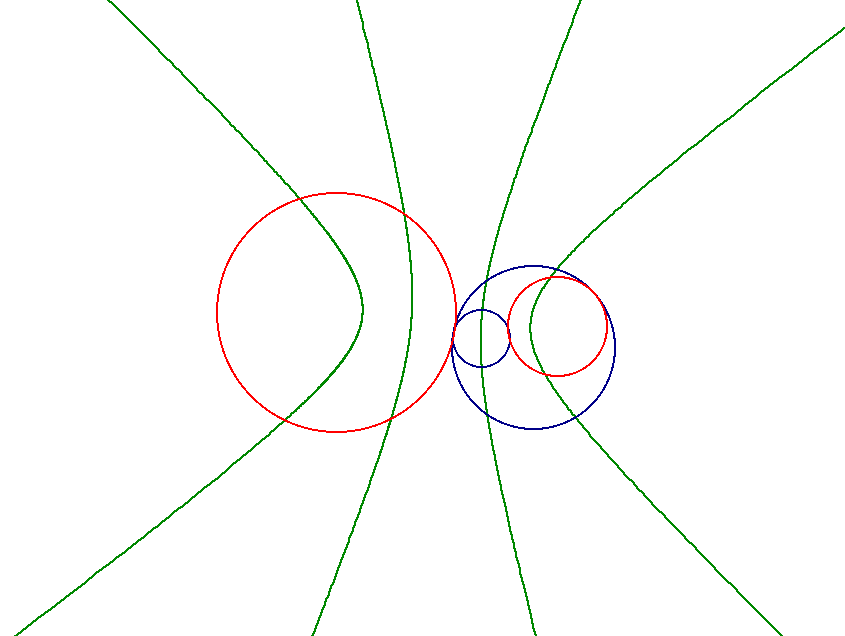
When we look at the next case which is when the given circles intersect at two points we see that the loci of the centers of the constructed circles appear to be an ellipse and a hyperbola.
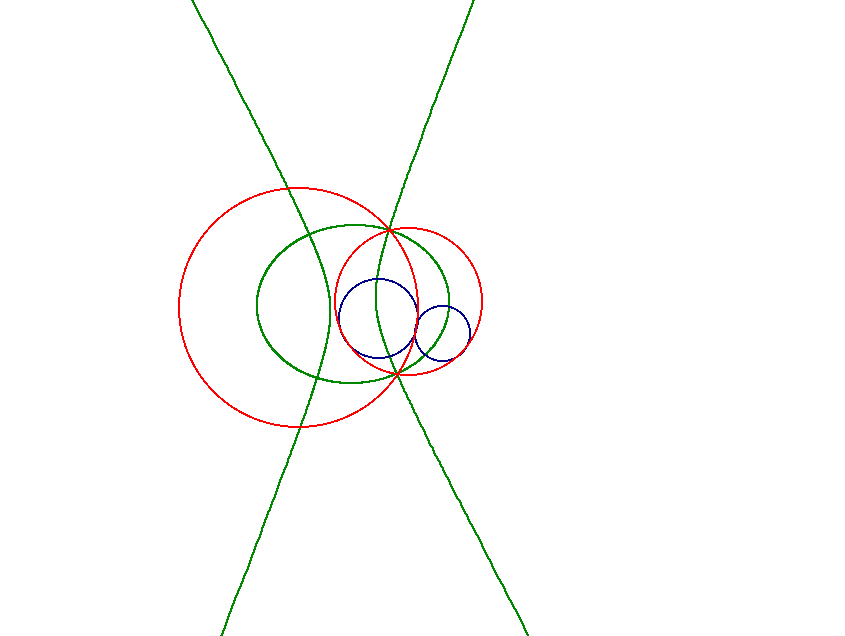
In fact, when the construction lines are drawn in, the proof to show that these loci are indeed what they appear to be is nearly identical to the cases before.
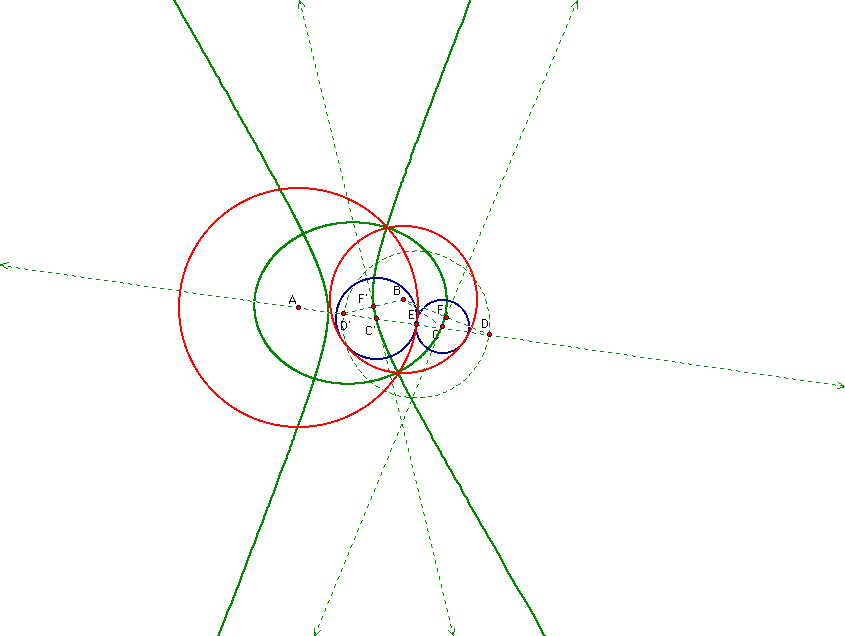
Since the proof is so similar to those done above, they are also left to the reader as practice.
This problem is a rich one indeed. That is because it doesn't have to stop here. What happens we when you want to find a tangent circle given a circle an a line, two ellipses, points on lines, etc? What do the loci of the centers of those constructed tangent circles look like? Can you prove what you suspect? Keep trying different circumstances and situations to learn more than you thought was possible.