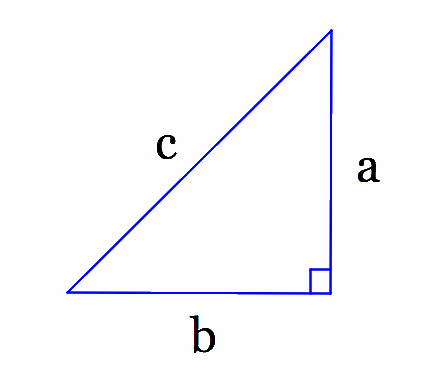
Pythagorean Theorem Unit
Georgia Performance Standard:
M8G2 : Students will understand and use the Pythagorean Theorem
a. Apply properties of right triangles, including the Pythagorean Theorem.
b. Recognize and interpret the Pythagorean Theorem as a statement about areas of squares on the sides of a right triangle.
Begin the unit by introducing some history of Pythagorous (A useful site: http://www-history.mcs.st-and.ac.uk/Biographies/Pythagoras.html). Allow for students to contribute any information they may already know. Now, write the theorem on the board:
For any right triangle, with sides a and b, and hypotenuse c, the square of the hypotenuse is equal to the sum of the squares of the two sides.
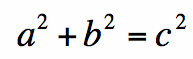
Allow time for students to discuss the presented theorem in small groups (or have a class discussion) and write or rephrase it in their own words. (Make sure to monitor their discussion very closely). The teacher may need to give a brief review of right, obtuse, and acute triangles.
The teacher should ask: "Will it work for any triangle such as obtuse or acute?" Ask students what they think, don't just ask the question - take a poll by hand or call on a particular student and ask what he or she suspects. Next students can explore a few examples with right, obtuse, and acute triangles. Students should now be given constructed triangles ranging from acute to obtuse and they are to measure (using a ruler) the sides of the triangles and compute the square of each leg and hypotenuse as well as the sum of the squares. The handout is attached below (the triangles were constructed using GSP). It is important to discuss the error that comes with measurement here. These measurements are not calculations! A Geometer's Sketchpad (GSP) document is attached as well. This should be used at the end of the activity. Change the lengths of the sides of the triangle and watch how the sum of the square of the sides stays the same as the square of the hypotenuse.
Handout solutions (measurements of triangles)
Students are given an opportunity in the task to make a hypothesis about the largeness or smallness of the angle corresponding to the hypotenuse and its relationship to how close the pythagorean theorem comes to being true for non-right triangles. Through GSP, they can explore (or this can be shown by the teacher) this for themselves. They should find that the further the angle is from 90 degrees, the further the theorem is from being true. (You could take this further and show that there is a relationship for acute and obtuse rectangle as it pertains to the Pythagorean Theorem - the sum of the legs squared are greater/less than the square of the hypotenuse).
Now students should try a few concrete examples to test their newly learned knowledge. For example, give them a right triangle with 2 given side lengths and have them calculate the hypotenuse. Do the same again, but leave out one of the sides and give them a leg and the hypotenuse. See below.
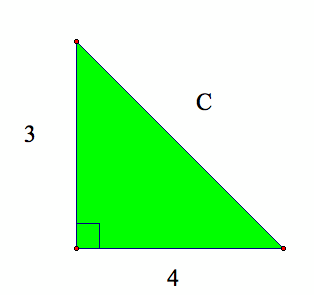
Example 1:
Find the missing length "c"
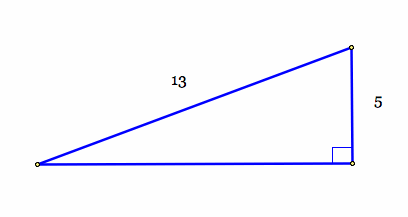
Example 2:
Find the missing length of the right triangle:
Now that students have seen some concrete examples, let's dig into the "why."
Consider the 2 figures below, they will be used in our proof.
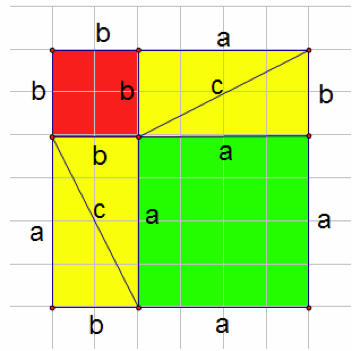Figure I 
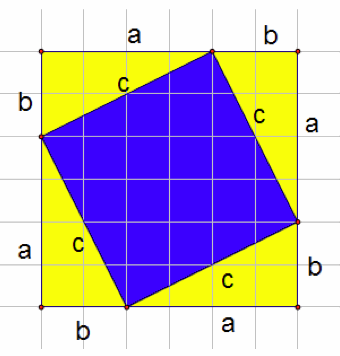Figure II
Using figure I, have students find the area of the green and red squares as well the yellow rectangles. They should easily deduce the area of the green square is 
, the red is 
, and each rectangle has an area of a*b. From here, they should calculate the total area of the larger square in Figure I which is the sum of each of the smaller areas:
=
The instructor should then lead them to find the area of the yellow triangles and the 'tilted' blue square in Figure II. They will find the area of the blue square is 
and each of the four yellow triangles has an area of (1/2)(a*b). The total area of the square in Figure II then is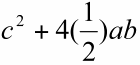 
= 
. If it has not already been addressed, recognize the two larger squares in Figure I and Figure II are equal, since each have a side length a+b. Therefore = . The most important point to make here is that sides a and b are also the sides of the right triangles in each figure, and c is the hypotenuse of each triangle. The students should be answering all of these questions and the teacher should act as a prompter.
Now let your students explore a little more! Allow them to divide into groups (or individually) and work through some interactive applets. A list with my 3 favorites is provided below.
http://www.ies.co.jp/math/java/geo/pitha1/pitha1.html
http://www.ies.co.jp/math/java/geo/pythasvn/pythasvn.html
http://www.pbs.org/wgbh/nova/proof/puzzle/theorem.html
The instructor can split students into small groups, each exploring the theorem through a different applet. After an appropriate period of time, each group can demonstrate their applet to the class and explain why the shapes fit, and how it displays the Pythagorean Theorem. Interactive learning helps solidify the students' understanding of the concept. They may have already been sure the shapes would fit, but actually trying for themselves and being able to manipulate the shapes will help them retain the newly learned information.
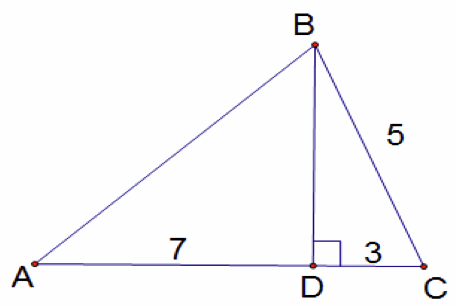
From here, students have been fully introduced to the concepts of the Pythagorean Theorem. Students should try a few more basic problems as well as problems requiring them to calculate the area of the triangle using the Pythagorean Theorem. In the diagram below, students can be asked to find the area of triangle ABC. To do so, they must use the Pythagorean Theorem to find the height BD.
The tasks are setting these students up for high school level mathematics and reasoning. Now, most importantly, the instructor should provide more worthwhile examples with real life applications of the Pythagorean Theorem, which are plentiful. For example, ask students to solve the following problem:
The cross-country team leaves the school and runs due south for 5 kilometers, they then turn and run due west for another 8 kilometers. What is the shortest possible distance they will have to travel to get back to school? (Round to the nearest hundredth)
There are numerous amounts of materials available to assist teachers in teaching the Pythagorean Theorem. Make use of them! Lessons on the Pythagorean Theorem can extended from the one above (dive into Pythagorean Triples - possible performance tasks). The lesson above should take a few class (2-3) periods and should not be rushed. This is a really important concept in mathematics that will continue to show itself to your students. A sound understanding of the Pythagorean Theorem will greatly help students understand later concepts in high school such as trigonometric identities and the distance formula.