
| This is the write-up of Assignment #9 |
Brian R. Lawler
|
| EMAT 6680 |
01/02/01
|
| See the Definition and Construction of a Pedal Triangle | |
|
II.
|
Exploring conditions of the Pedal Triangle |
| Considering various loci and traces |
(Click on image to explore in Geometer's Sketchpad.)
| 2. | What if pedal point P is the centroid of triangle ABC? | |
| When the pedal point is located at the centroid of triangle ABC, it appears that the pedal triangle will always exist inside the original triangle. | 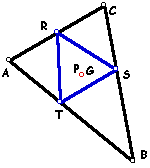 |
|
| 3. | What if . . . P is the incenter . . . ? | |
| When the pedal point is located at the incenter of triangle ABC, points R, S, and T lie at the points of tangency of triangle ABC's incircle. Thus, this incircle is also the circumcircle of triangle RST. | 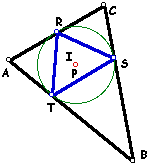 |
|
| 4. | What if . . . P is the Orthocenter . . . ? Even if outside ABC? | |
| When the pedal point is located at the orthocenter of triangle ABC, the points R, S, T occur at the intersection of triangle ABC's sides and altitudes. | 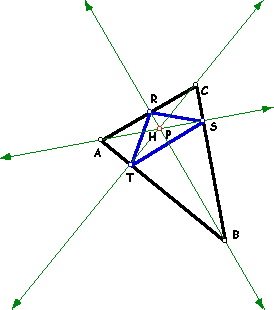 |
|
| 5. | What if . . . P is the Circumcenter . . . ? Even if outside ABC? | |
| When the pedal point is located at the circumcenter of triangle ABC, the points R, S, T occur at the midpoints of triangle ABC's sides. | 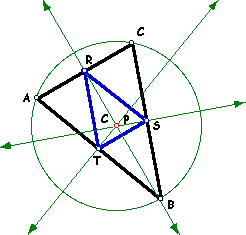 |
|
| 6. | What if . . . P is the Center of the nine point circle for triangle ABC? | |
| Recall triangle ABC must be acute for the nine point center to exist. When the pedal point is located at this center, the points R, S, and T all lie on the sides of triangle ABC. | 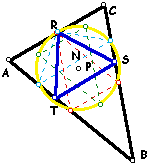 |
|
| 7. | What if P is on a side of the triangle? | Click here to investigate the GSP file. |
| Again, R, S, and T will always remain on triangle ABC. | ||
| 8. | What if P is one of the vertices of triangle ABC? | |
| 9. | Find all conditions in which the three vertices of the Pedal triangle are colinear (that is, it is a degenerate triangle). This line segment is called the Simson Line. | |
| The pedal triangle degenerates as P becomes one of the points A, B, or C. | 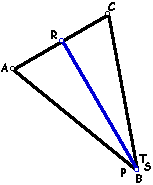 |
 |
Comments? Questions? e-mail me at blawler@coe.uga.edu |
| Last revised: January 2, 2001 |
|