
| This is the write-up of Assignment #9 |
Brian R. Lawler
|
| EMAT 6680 |
01/02/01
|
| See the Definition and Construction of a Pedal Triangle | |
| Exploring conditions of the Pedal Triangle | |
|
III.
|
Considering various loci and traces |
(Click on image to explore in Geometer's Sketchpad.)
| 10. | Locate the midpoints of the sides of the Pedal Triangle. Construct a circle with center at the circumcenter of triangle ABC such that the radius is larger than the radius of the circumcircle. Trace the locus of the midpoints of the sides of the Pedal Triangle as the Pedal Point P is animated around the circle you have constructed. What are the three paths? | |
| The locus of each midpoint appears to be an ellipse. With a little further investigating, it appears that this is not restricted to circles larger than the circumcircle. | 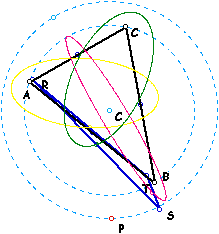 |
|
| 11. | Repeat where the path is the circumcircle? | |
| Again, the locus of each midpoint appears to be an ellipse. What has changed is that the pedal triangle is now a Simson's Line. | 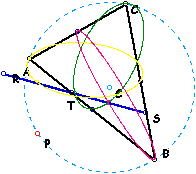 |
|
| 11a. | Construct lines (not segments) on the sides of the Pedal triangle. Trace the lines as the Pedal point is moved along different paths. | Click here to view GSP file. |
| 11b. | In particular, find the envelope of the Simson line as the Pedal point is moved along the circumcircle. Note, you will need to trace the image of the line, not the segment. | 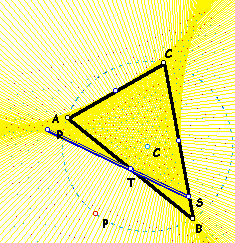 |
| 12. | Repeat where the path is a circle with center at the circumcenter but radius less than the radius of the circumcircle. | |
| The result in 11b. above appears much nicer. The locus is complete in a sense - as opposed to the incomplete coverage of the plane in this new situation. | 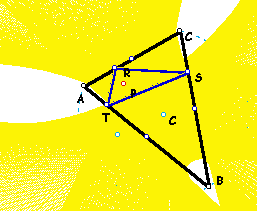 |
 |
Comments? Questions? e-mail me at blawler@coe.uga.edu |
| Last revised: January 2, 2001 |
|