

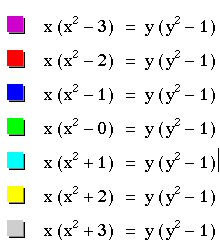
In this investigation we are asked to examine:
![]() for n in this case to be from -3 to
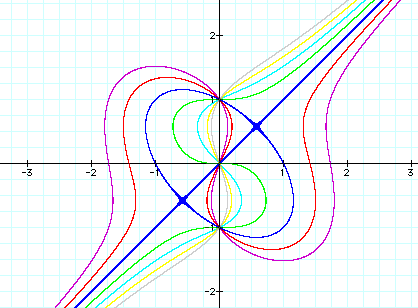
+3.As n grows large the graph disconnects at the intersection
of the ellipse like figure and the line. Also the graph becomes
very curvy. As n gets very negative the graph looks as if it is
trying to straighten out, however it is "pined down"
at (0,1) and (0,-1) . As noted,
something very interesting happens when n =1 i.e
for n in this case to be from -3 to
+3.As n grows large the graph disconnects at the intersection
of the ellipse like figure and the line. Also the graph becomes
very curvy. As n gets very negative the graph looks as if it is
trying to straighten out, however it is "pined down"
at (0,1) and (0,-1) . As noted,
something very interesting happens when n =1 i.e ![]() .
From the equation, it can be noted that there are two equations
meeting at two points which is evidenced by the existence of the
nods at the point of intersection. If the two equations meet then,
they can be factorized so that more investigations can be made.
Note that the equation can be factorized further i.e
.
From the equation, it can be noted that there are two equations
meeting at two points which is evidenced by the existence of the
nods at the point of intersection. If the two equations meet then,
they can be factorized so that more investigations can be made.
Note that the equation can be factorized further i.e ![]() which
means this equation is made of two equations which meet at given
points as shown below.
which
means this equation is made of two equations which meet at given
points as shown below.
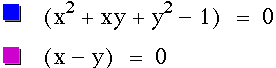
 .
.To carry out more investigation
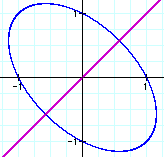
, it is noted that the line Y = X intersect the equation ![]() which seems to looks
like an ellipse centered at (0,0) with its intercepts at points
(0,-1), (1,0), (0,1) and (-1,0). Click here
to proof that the equation
which seems to looks
like an ellipse centered at (0,0) with its intercepts at points
(0,-1), (1,0), (0,1) and (-1,0). Click here
to proof that the equation ![]() is ellipse.
with center (0,0). For more illustration click Graphing
calc #
is ellipse.
with center (0,0). For more illustration click Graphing
calc #
What will happen when we decide to add a constant to each side of the graph?
When we add a constant to each side of the equation we will get different slices through the 3 dimensional surface given by the equation
![]()
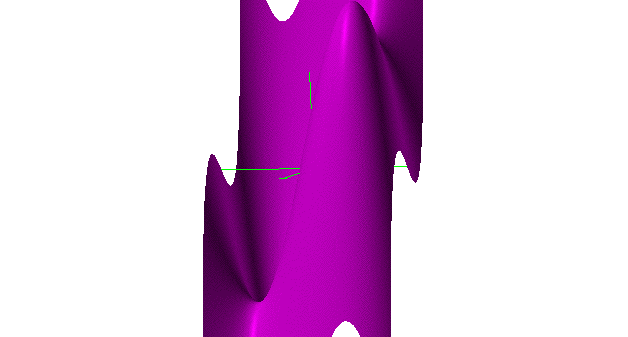
Take a look at the graph of this surface.
Back homepage