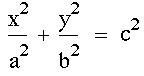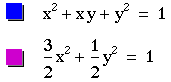by
Samuel Obara
Proof that the equation
by
Samuel Obara
Proof that the equation  Is ellipse
The general equation
of a conic section is
Is ellipse
The general equation
of a conic section is 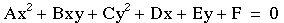
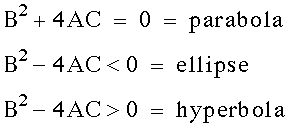
It should be noted that the
ellipse is not symetrical neither in the x-axis nor the y-axis
therefore we need a transformation so that it can be symetrical
along the x and y axis with center (0,0).
To transform the equation,
we need to use the following equations
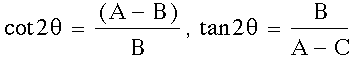 which means the values
of X and Y will be
which means the values
of X and Y will be
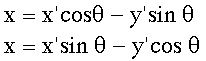 therefore in the equation
therefore in the equation A = 1, B = 1 C = 1 by using the discriminant
A = 1, B = 1 C = 1 by using the discriminant
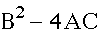 then
then 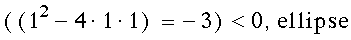
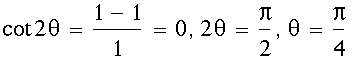
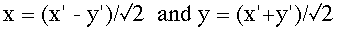 substitute x and y
in
substitute x and y
in
 it becomes
(x')^2 - 2x'y' + (y')^2
+ (x')^2 - (y')^2 + (x')^2 + 2x'y' + (y')^2 = 2
therefore
3(x')^2 + (y')^2 =
2 which means
{3(x')^2}/2 + {(y')^2}/2
= 1
(x')^2}/(2/3) + {(y')^2}/2
= 1
it becomes
(x')^2 - 2x'y' + (y')^2
+ (x')^2 - (y')^2 + (x')^2 + 2x'y' + (y')^2 = 2
therefore
3(x')^2 + (y')^2 =
2 which means
{3(x')^2}/2 + {(y')^2}/2
= 1
(x')^2}/(2/3) + {(y')^2}/2
= 1
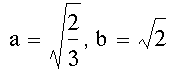 which
agrees with the general equation of ellipse:
which
agrees with the general equation of ellipse:
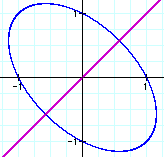
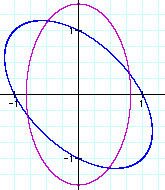
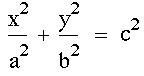 note if we plot the
two equations, we obtain the following graph.
note if we plot the
two equations, we obtain the following graph.
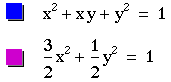
 Which means the equation
Which means the equation
 is ellipse.
is ellipse.
Back to assign # 1 page


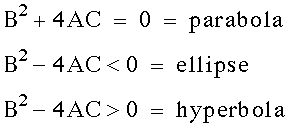

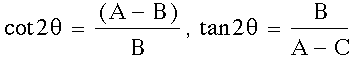
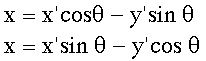
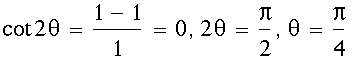
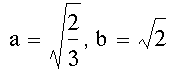 which
agrees with the general equation of ellipse:
which
agrees with the general equation of ellipse: