
Where did Tesselations Come From?
In Mathematics
Although tessellations have been traced back to ancient human cultures and
can also be found in the natural world, they have had a relatively short history
as a topic for serious mathematical and scientific study. One of the first
mathematical studies of tessellations was conducted by Johannes Kepler in
1619 who wrote about the regular and semiregular tessellation, which are coverings
of a plane with regular polygons. However, about two hundred years passed
before new scientific progress concerning tessellations was made.
Near the end of the nineteenth century in 1891, the Russian crystallographer
E. S. Fedorov proved that every tiling of the plane is constructed in accordance
to one of seventeen different groups of isometries (i.e., methods of repeating
tilings over the plane). His study marked the unofficial beginning of the
mathematical study of tessellations, occurring only about a hundred years
ago. Progress beyond this point has resulted in advanced mathematical analyses
of tilings (e.g., extending tilings to more than two dimensions and to non-Euclidean
geometrical systems) which can be only hinted at in the Beyond section of
this site. Prominent names and dates in this research area include the following:
Shubnikov and Belov (1951); and Heinrich Heesch and Otto Kienzle (1963).
In Science
Aside from being studied in mathematical or geometrical research, tessellations
and tilings have been linked with x-ray crystallography. X-ray crystallography
is a field of science concerned with the repeating arrangements of identical
objects as found in nature, a description very similar to the geometrical
definition of tessellation. Interestingly, the discoveries made in x-ray crystallography
during the mid-20th century are similar to many of the discoveries the Dutch
artist M. C. Escher made while formulating designs for his tessellated artwork.
(Click here for more about Escher.)
The symmetry issues that are so important in tessellations have shown to be relevant to quantum mechanics, the study of particles smaller than atoms.
Several other scientific and engineering applications have been found for tessellations. For instance, tiling research has benefited the conservation of sheet material and reduction of scrap metal. How? The closer fitted that the objects to be cut out are, the less waste material produced. Since tessellations are perfectly fitted patterns of shapes, no waste material would be produced if the template resembled a tessellation.
Other fields of research associated with tiling include geology, metallurgy, biology, and cryptology (the study of using secret codes in communication).
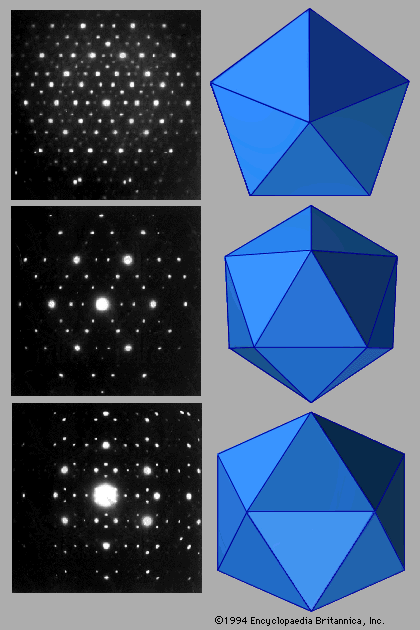 |
This image suggests the relationship between tessellations, symmetry,
and x-ray crystallography. Original Caption: Figure 16: (Left) Electron diffraction patterns of quasicrystalline aluminum-manganese. (Top left) View is along the fivefold symmetry axis; (centre left) rotating by 37.38 reveals the threefold axis, and (bottom left) rotating by 58.29 reveals the twofold axis. (Right) Corresponding views of icosahedrons show that quasicrystalline symmetries match those of the icosahedrons. (Left) D. Shechtman, Physical Review Letters, vol. 53, no. 20, Nov. 1984 reprinted with permission from Encyclopaedia Britannica |
Resource Page: http://library.thinkquest.org/16661/index2.html
Return to the Tesselation Home Page