p » Ö(40/3 – 2Ö3) » 3.14153
In the first approximation,
we will construct a segment having a length of approximately 3.14153, which is
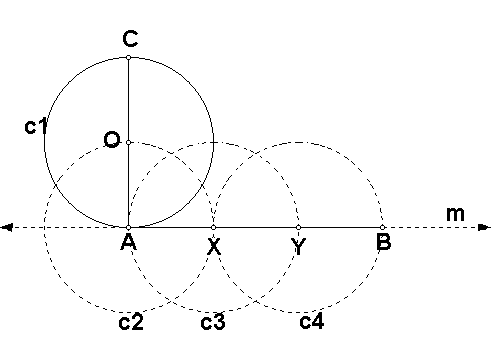
a little more than p - 0.00006. Suppose we are given a circle c1
with radius OA = 1. Construct the
diameter CA of circle c1. We
want to construct a segment AB tangent to circle c1 at the point A
so that the length of AB is 3. To
construct the segment AB, first construct the line m perpendicular to AO
through A. Construct the circle c2
with center A though O. Construct one
of the intersection points of the circle c2 and the line m, and
label it X. Construct the circle c3
with center X through A. Construct the
point of intersection of circle c3 and the line m (that is not the
point A), and label it Y. Construct the
circle c4 with center Y through the point X. Construct the point of intersection of
circle c4 and the line m, and label it B. Construct the segment AB.
Since the four circles are congruent, OA = AX = XY = YB = 1, so AB =
3.
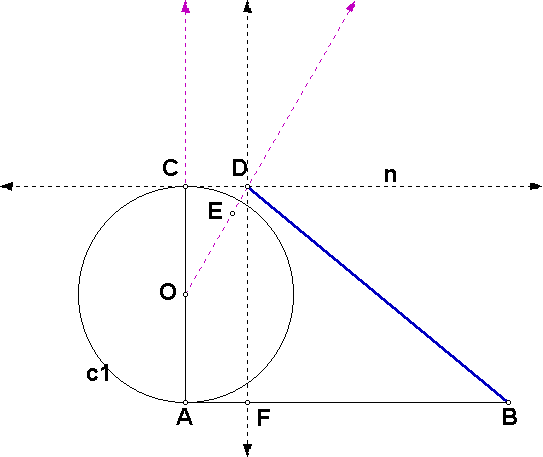
Construct the line n through C parallel to AB. Using the script for the construction of a 30° angle, construct the angle EOC such that the measure of angle EOC = 30°. Construct the intersection of line n and ray OE, and label it D. Construct the segment BD. The length of BD is approximately 3.14153.
Why does this construction
work?
Consider
right triangle OCD. The circle c1
has a radius of length 1, so OC = 1.
Angle DCO is a right angle, so tan(ÐCOD) = tan(30°) = CD/OC = CD. Therefore, CD = tan(30°) = Ö3/3.
Now drop a perpendicular from point D to segment AB, and let the foot of the perpendicular be F. Consider the triangle BDF. Since the length of CD is Ö3/3, the length of AF is also Ö3/3. The length of AB is 3 (by construction), so the length of BF is 3 - Ö3/3. Applying the Pythagorean Theorem to triangle BDF, we have
(BD)2 =
(DF)2 + (BF)2 = 22 + (3 - Ö3/3)2 = 4 + 9 – 2Ö3 + 1/3 = 40/3 – 2Ö3.
Therefore,
BD = Ö(40/3 – 2Ö3) » 3.14153.
Now
that we have a segment of length p (approximately), we need to
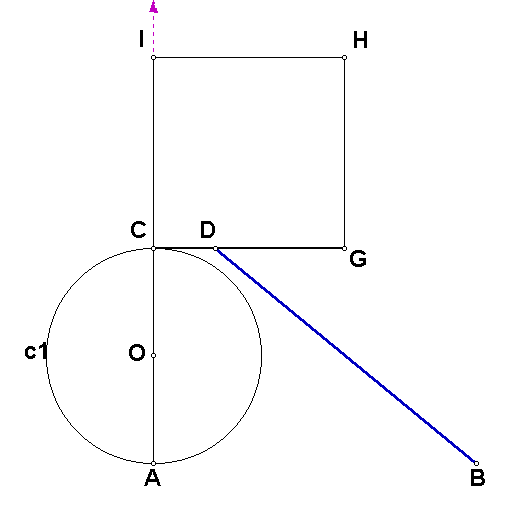
construct a square having sides of length Öp. Use
the script to construct segment CG having length ÖBD. (OC = 1 and BD = x.) Use the script for constructing a square to
construct a square having side CG. The
area of square CGHI is approximately equal to the area of circle c1.
Click here for a GSP sketch of
the construction.