

Given line segment AB, construct perpendicular lines to the segment through the given endpoints. Choose a point D above the segment on either perpendicular and construct a parallel line to segment AB.

Construct the midpoint of segment CD and label it M. Construct segments DB and AM. Label their intersection point G.
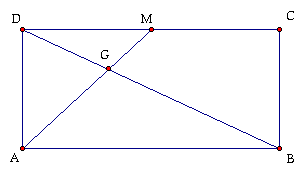
Construct the perpendicular line segment from G to segment AB. Label this point X.

To continue on bisecting the segment,click
on the following:
1/5's
1/7's
The even partitions
are constructed by using the same procedures as above. The only
difference coming with the construction of A to the midpoint of
DC. That line segment should simply be another diagonal, AC, intersecting
the diagonal BD. From there, the order of partitioning the segment
remains constant to that above.