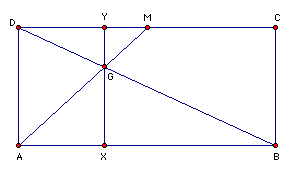
Prove : AX = (1/3)AB

Triangle DGM ~ Triangle BGA {by the AA Theorem of Similar Triangles}
DM = (1/2)DC {Def. of midpoint}
DC = AB {Prop. of Rectangles}
DM = (1/2)AB {Substitution}
DM/AB = 1/2 {Division}
GY/GX = 1/2 {Prop. of Similar Triangles}
Triangle MGY ~Triangle AGX {AA}
MY/AX = GY/GX {Proportional parts of similar triangles}
MY/AX = 1/2 {Substitution}
AX = DY {Prop. of rectangles}
MY/DY = 1/2 {Substitution}
MY/DY + 1 = 1/2 + 1 {Addition}
(MY + DY)/DY = 3/2 {Simplification}
DM/DY = 3/2 {Segment Addition}
DY/DM = 2/3 {Prop. of proportions}
DY = (2/3)DM = (2/3)(1/2)AB = (1/3)AB {Substitution,Multiplication}
AX = (1/3)AB {Substitution}
BACK