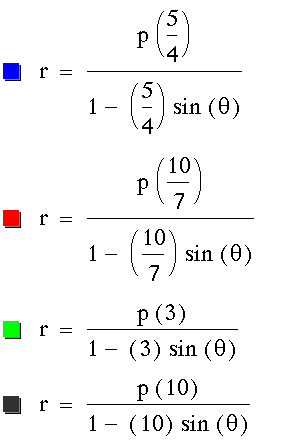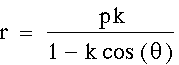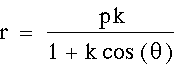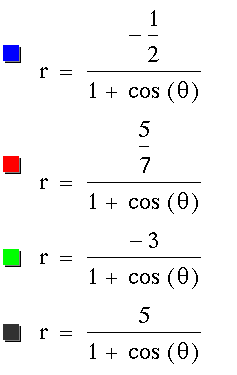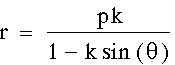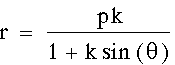Explorations with
Polar Equations
by: Lauren Wright
In this investigation, we look at the
following equations with different values of p.
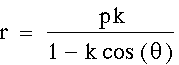 ,
, 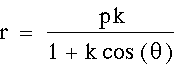 ,
,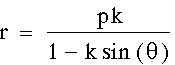 , and
, and 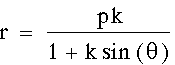 .
for k > 1, k = 1, and k < 1.
Note: The parameter k is called the
"eccentricity" of these conics. It is usually called
"e" but for many software programs e is a constant and
can not be set as a variable.
For notes on a derivation of these
formulas, see Dr. Jim Wilson's page by clicking here.
.
for k > 1, k = 1, and k < 1.
Note: The parameter k is called the
"eccentricity" of these conics. It is usually called
"e" but for many software programs e is a constant and
can not be set as a variable.
For notes on a derivation of these
formulas, see Dr. Jim Wilson's page by clicking here.
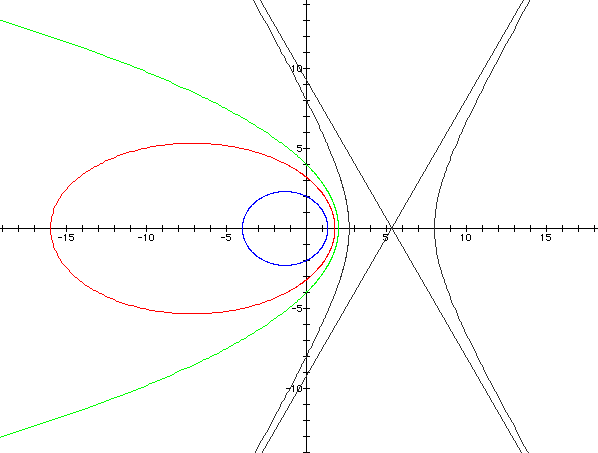
First, let's take a look at 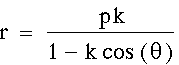 for
k < 1 and p = -4.
for
k < 1 and p = -4.
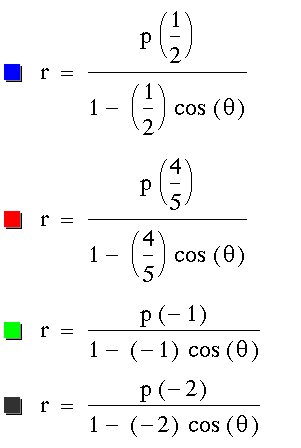
 For p = 2, we get the following:
For p = 2, we get the following:
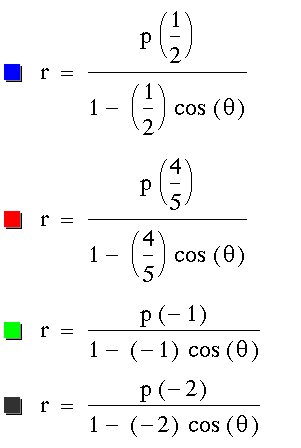
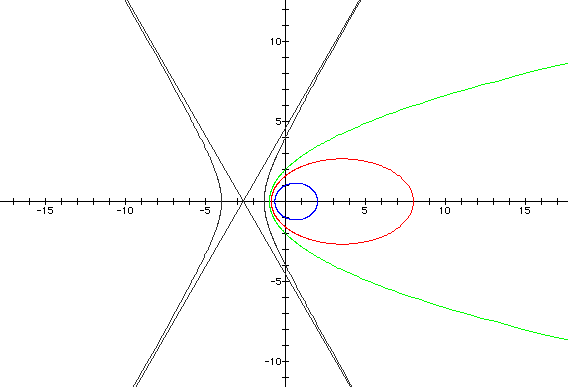 To investigate these graphs on your
own, click here to download a Graphing
Calculator file.
*I chose p = -4 and p = 2 arbitrarily
for illustration purposes. You can download the files to vary
p on your own.
To investigate these graphs on your
own, click here to download a Graphing
Calculator file.
*I chose p = -4 and p = 2 arbitrarily
for illustration purposes. You can download the files to vary
p on your own.
Now let's do the same thing for 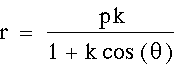 .
for k < 1 and p = -4
.
for k < 1 and p = -4
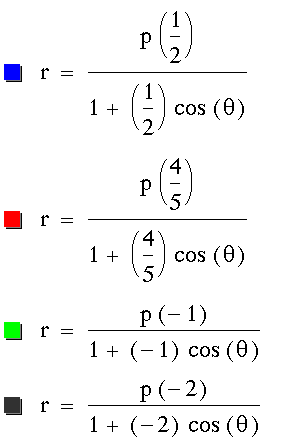
 for k < 1 and p = 2
for k < 1 and p = 2
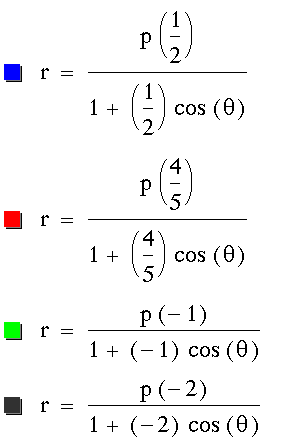
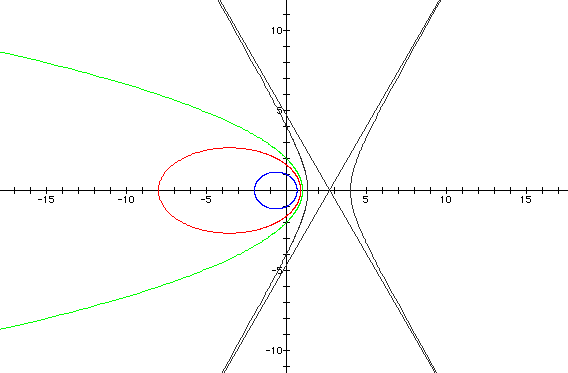 To investigate this on your own, click
here.
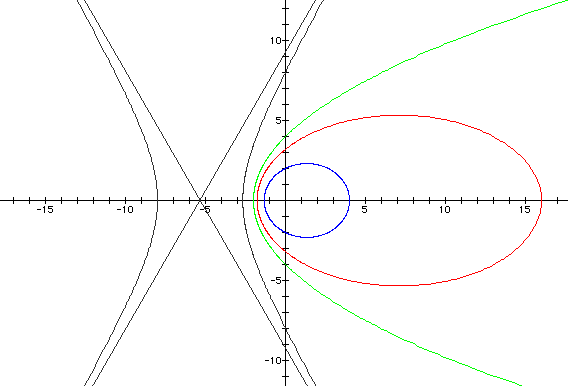
For these illustrations, we see that
if
To investigate this on your own, click
here.
For these illustrations, we see that
if 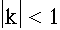 , an ellipse is formed. If k =
-1, a parabola is formed. And, if k < -1, a hyperbola is formed.
All of these conic sections have focal points lying on the x-axis.
**NOTE: The straight lines on the gray graphs
are asymptotes - they are not part of the actual graph.
, an ellipse is formed. If k =
-1, a parabola is formed. And, if k < -1, a hyperbola is formed.
All of these conic sections have focal points lying on the x-axis.
**NOTE: The straight lines on the gray graphs
are asymptotes - they are not part of the actual graph.
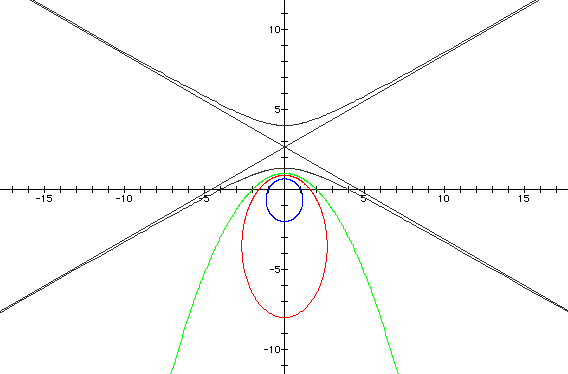
Next, let's take a look at 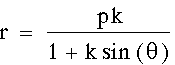 for k < 1.
for k < 1 and p = -4
for k < 1.
for k < 1 and p = -4

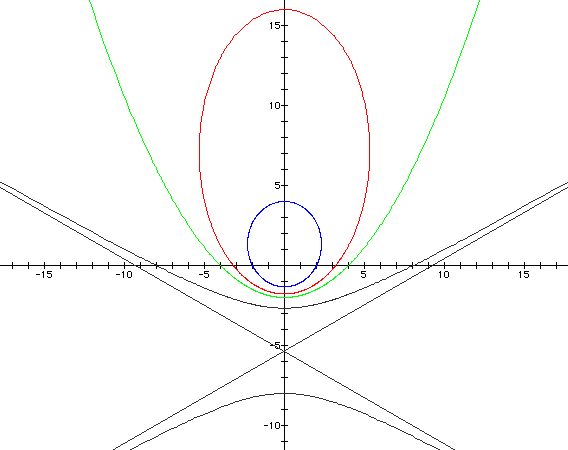 for k < 1 and p = 2
for k < 1 and p = 2
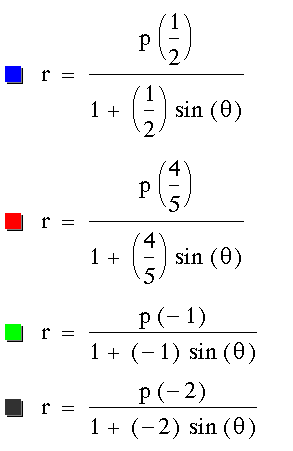
 To investigate this on your own, click
here.
To investigate this on your own, click
here.
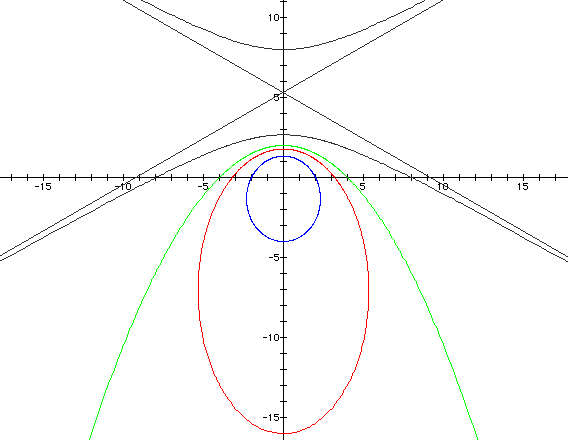
Repeating the process for 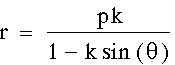 gives us the following...
for k < 1 and p = -4
gives us the following...
for k < 1 and p = -4
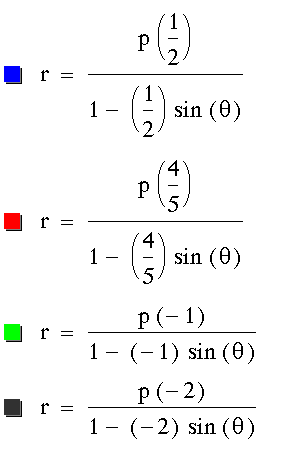
 for k < 1 and p = 2
for k < 1 and p = 2
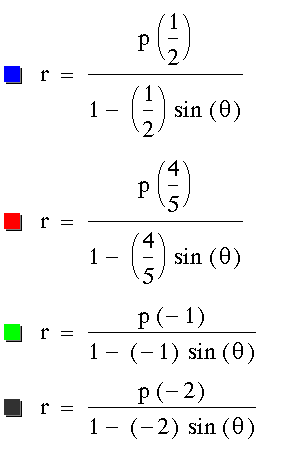
 To investigate this on your own, click
here.
We see that the same thing occurs with
To investigate this on your own, click
here.
We see that the same thing occurs with
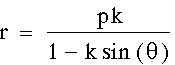 and
and 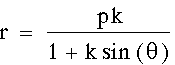 as
did before. The only difference is that the focal points lie on
the y-axis.
as
did before. The only difference is that the focal points lie on
the y-axis.
NOW, let's look at what happens when
k > 1.
For 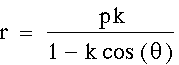 and
p = -4
and
p = -4
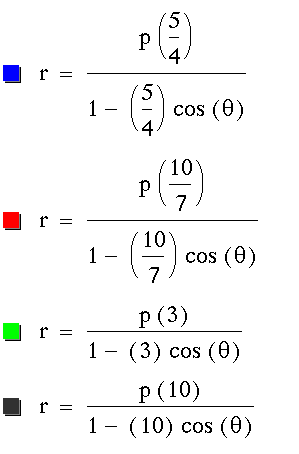
 For
For 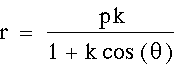 and
p = 2
and
p = 2
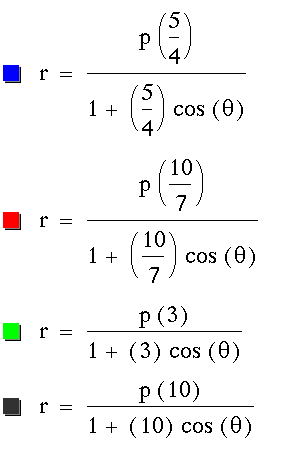
 For
For 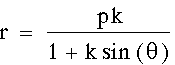 and
p = -4
and
p = -4
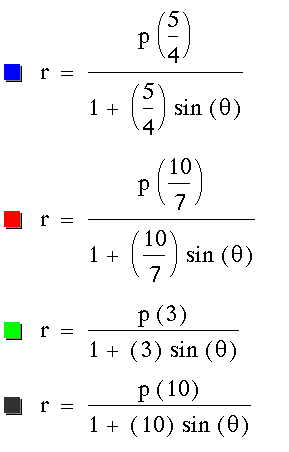
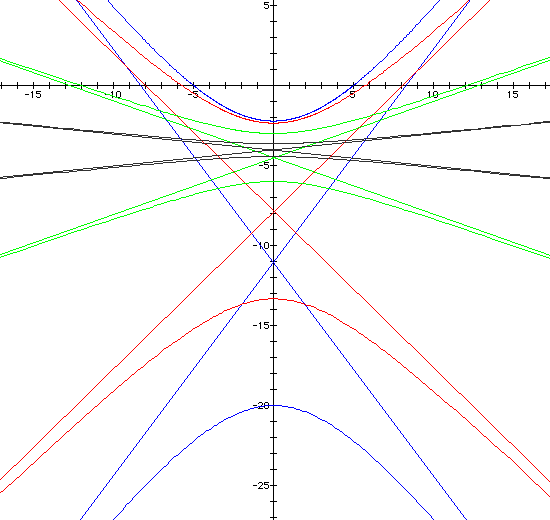 For
For 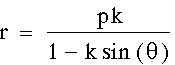 and
p = 2
and
p = 2
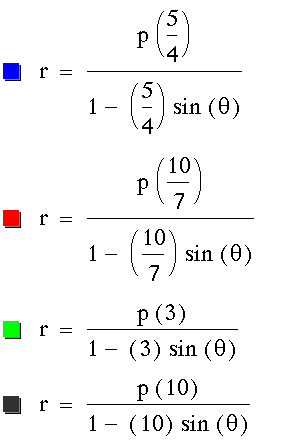
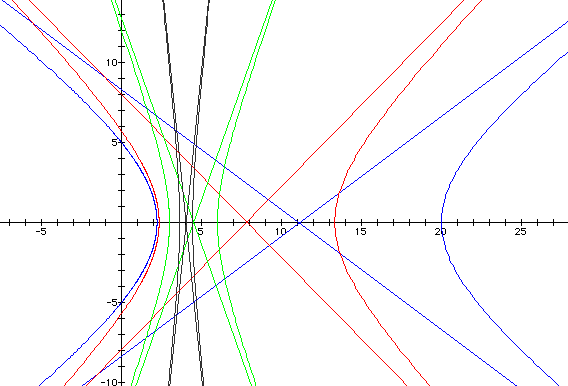
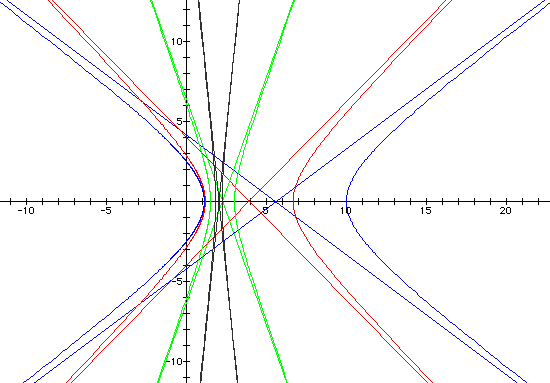
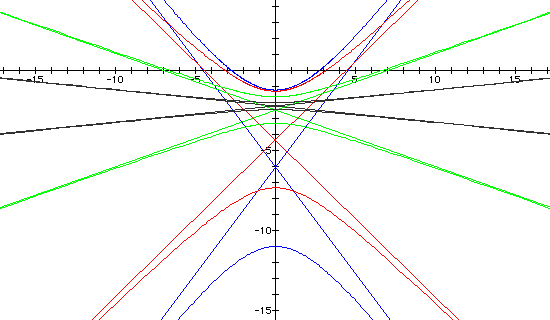 We can conclude that when k > 2,
hyperbolas are formed. When there is a cosine in the denominator,
the focal points lie on the x-axis. When there is a sine in the
denominator, the focal points lie on the y-axis.
We can conclude that when k > 2,
hyperbolas are formed. When there is a cosine in the denominator,
the focal points lie on the x-axis. When there is a sine in the
denominator, the focal points lie on the y-axis.
For our last and final case, we will
explore what happens when k = 1.
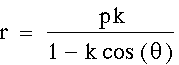
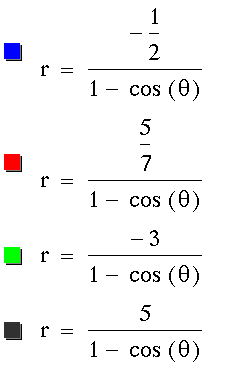
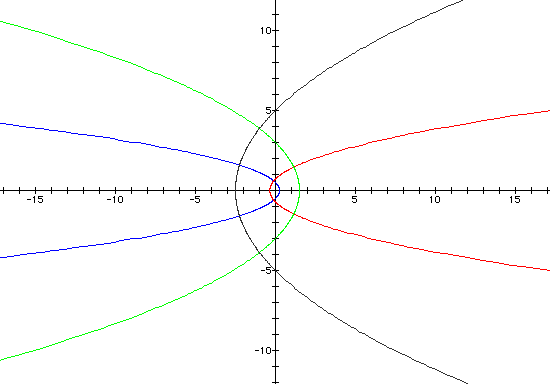
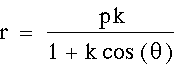
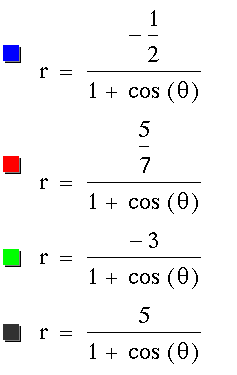
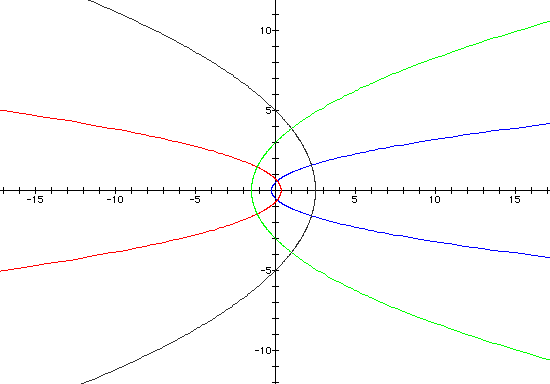
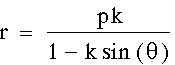
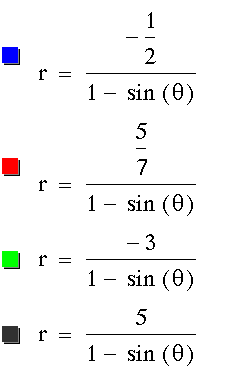
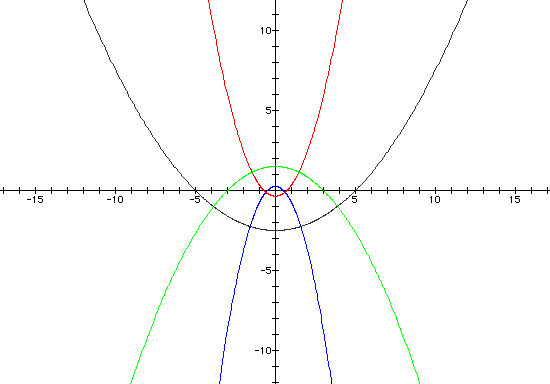
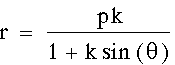

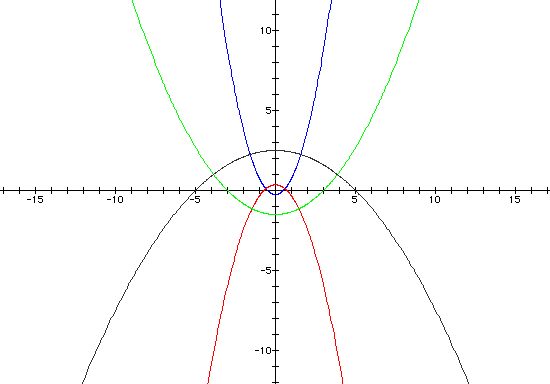 Finally, when k = 1, we get only parabolas
for varying values of p. When there is a cosine in the denominator,
the focal point lies on the x-axis. When there is a sine in the
denominator, the focal point lies on the y-axis.
Finally, when k = 1, we get only parabolas
for varying values of p. When there is a cosine in the denominator,
the focal point lies on the x-axis. When there is a sine in the
denominator, the focal point lies on the y-axis.
Return
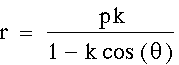 ,
, 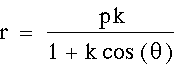 ,
,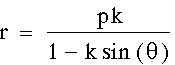 , and
, and 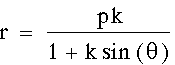 .
.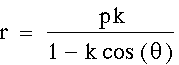 ,
, 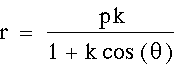 ,
,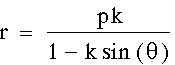 , and
, and 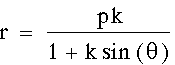 .
.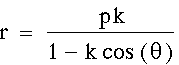 for
k < 1 and p = -4.
for
k < 1 and p = -4.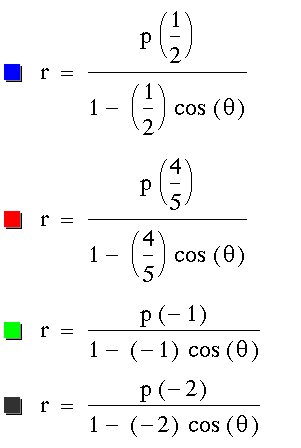

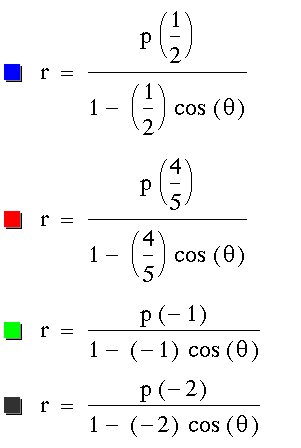

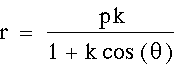 .
.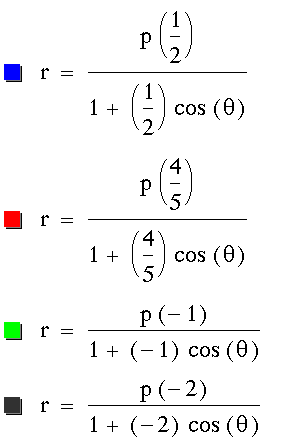

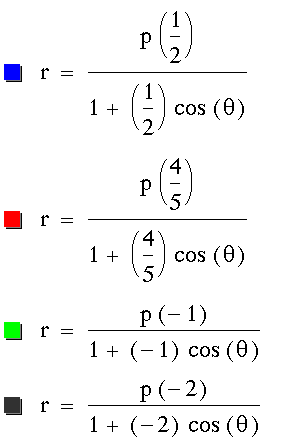

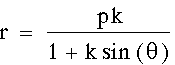 for k < 1.
for k < 1.

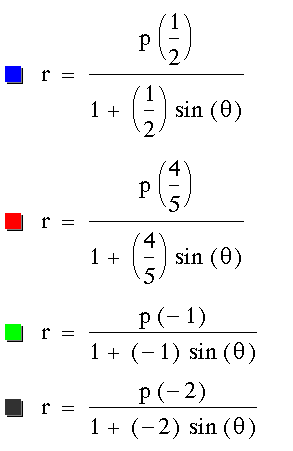

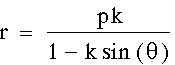 gives us the following...
gives us the following...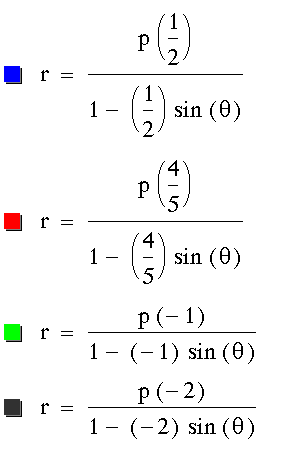

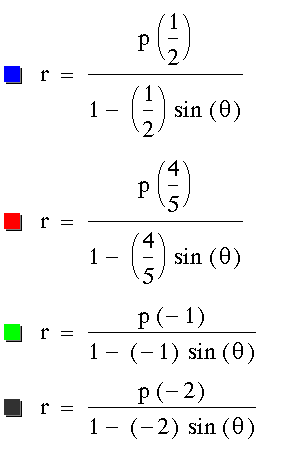

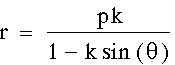 and
and 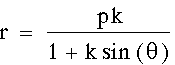 as
did before. The only difference is that the focal points lie on
the y-axis.
as
did before. The only difference is that the focal points lie on
the y-axis.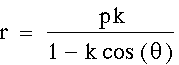 and
p = -4
and
p = -4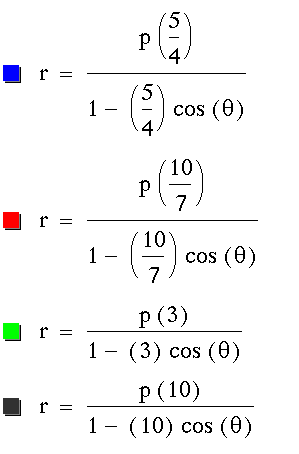

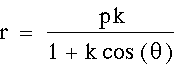 and
p = 2
and
p = 2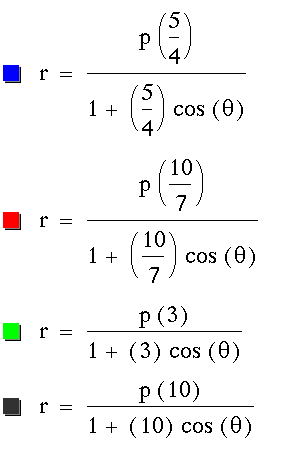

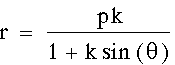 and
p = -4
and
p = -4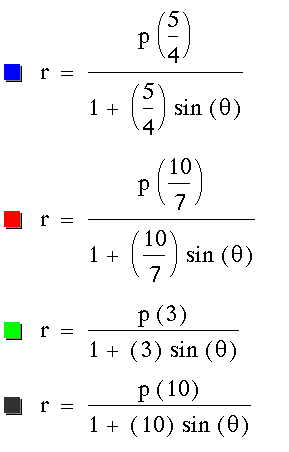

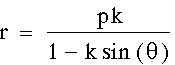 and
p = 2
and
p = 2