

Consider two points (3,4) and (-5,-2). For any point (x,y) we can write the distance equation. The first distance equation would appear in this form:
When this equation is graphed the graph appears as:
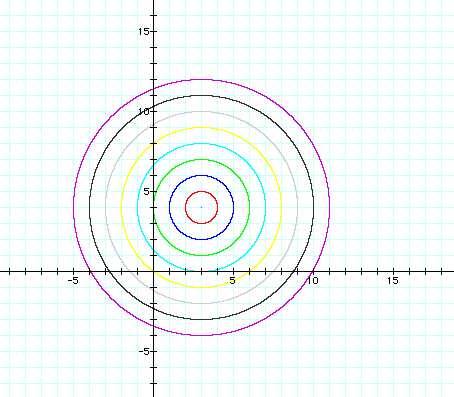
When the values of D ranges from 0-8 and are labeled as so:
To see a graph with greater values click here (QuickTime Player).
The second equation would appear as
When this equation is graphed the graph appears as:

When the values of D range from 0-8 and the labels are as follows
To see an illustration of this with greater values click here. (QuickTime Player)
a. Considering each graph when it is set to a non-zero constant would give the circles above without the points in the centers. They appear like:
and like
When the values of D range from 1-8. The difference that should be noticed between these two graphs and the graphs listed above is that removing the zero label from the graph produces the same graph without the zero value which was the point in the center of each graph.
b. Consider the sum for various values of C.
The graph when the C value is varied from 10 to 50 gives a representation
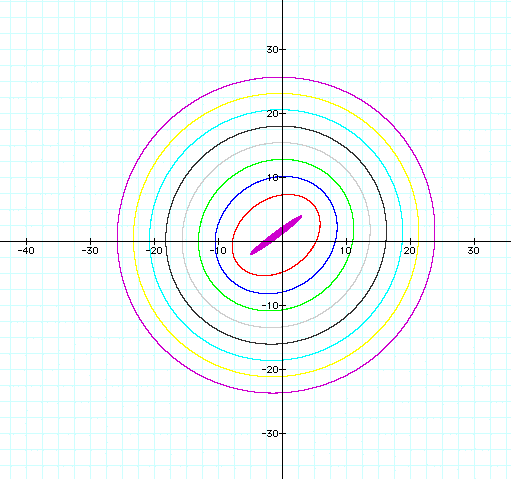
With the values labeled below:
To see an illustration with great values click here. (QuickTime Player)
c. Consider the product for various values of C.
The graph when the C value is varied from 1-40 gives a representation
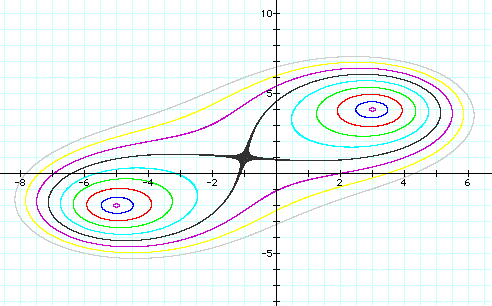
With the values labeled below:
To see an illustruation with greater values click here (QuickTime Player)
If you would like an explanation as to what is happening in the graphs above please click here.