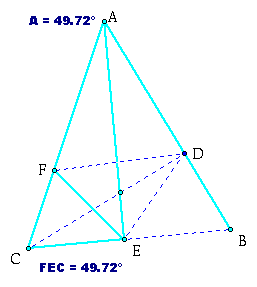
We start with the original triangle:
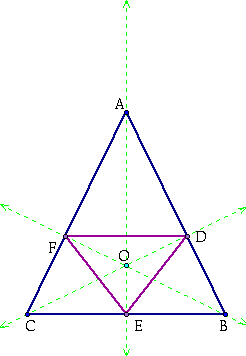
Now what we are going to do is prove that
![]() A =
A =![]() FEC.
We are going to do this by looking at quadrilateral OFCE.
FEC.
We are going to do this by looking at quadrilateral OFCE.
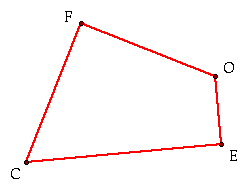
Since this quadrilateral is inscribed
in the triangle and formed by the perpendiculars, we know that
![]() F and
F and ![]() E,
are right angles.
E,
are right angles.
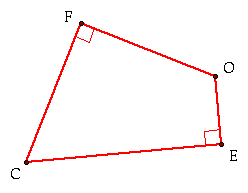
Additionally looking back, if we connect
EF and OC, we see that ![]() FCO and
FCO and ![]() FEO
(in orange) both share arc OF.
FEO
(in orange) both share arc OF.
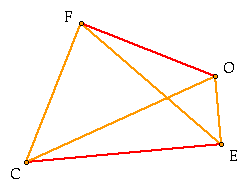
Therefore, ![]() FCO
=
FCO
= ![]() FEO (
FEO (![]() ACD
=
ACD
= ![]() FEA). Now look at triangle ACD.
FEA). Now look at triangle ACD.
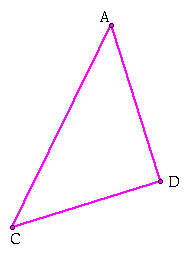
We know that triangle ACD is a right triangle,
since D is one of the perpendiculars and therefore a right angle.
Due to this fact we know that ![]() A and
A and
![]() C must therefore add to 90 degrees
(
C must therefore add to 90 degrees
(![]() A and
A and ![]() C
are complementary).
C
are complementary).
Now look at the figure below:
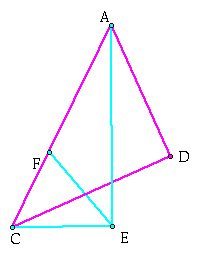
We additionally can see that since ![]() E forms a right angle, we know that
E forms a right angle, we know that ![]() CEF must be complementary with
CEF must be complementary with ![]() FEA.
Now since above we showed that
FEA.
Now since above we showed that ![]() ACD
(
ACD
(![]() FCO) was equal to
FCO) was equal to ![]() FEA
(
FEA
(![]() FEO), we must conclude that
FEO), we must conclude that ![]() FEC =
FEC = ![]() A. This
is the second part of what we needed to show.
A. This
is the second part of what we needed to show.