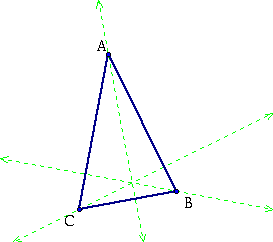
We first must draw the perpendicular bisectors (altitudes) of triangle ABC
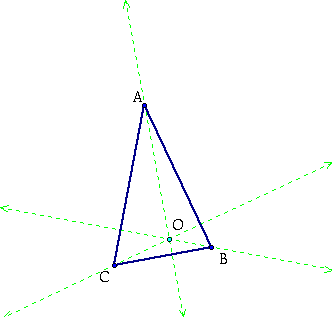
Next where the three altitudes connect, forms the orthocenter, labeled O.
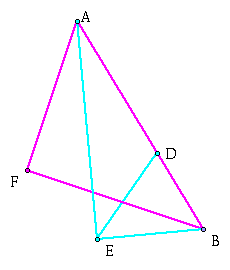
Now we can go ahead and label the points at which the altitudes cross the sides of triangle ABC, we will label these points D, E, and F.
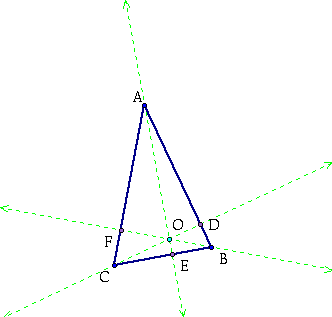
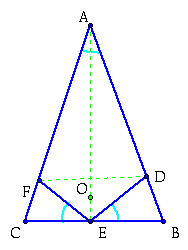
Now points D, E, and F, will form a triangle:
Now what we did to prove, is that the
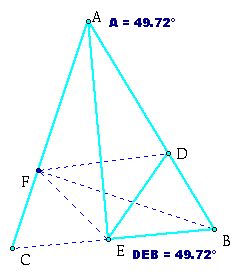
![]() FEC is equal to
FEC is equal to ![]() DEB, and that both of these
angles are equal to
DEB, and that both of these
angles are equal to ![]() CAB. We are going to do this by looking
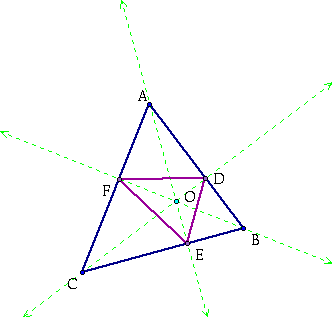
at quadrilateral ODBE.
CAB. We are going to do this by looking
at quadrilateral ODBE.
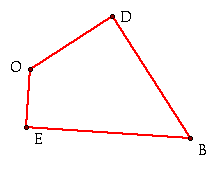
Since this quadrilateral is inscribed
in the triangle and formed by the perpendiculars, we know that
![]() E and
E and ![]() D, are right angles.
D, are right angles.
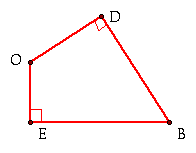
Additionally looking back, if we connect
DE and OB, we see that ![]() DBO and
DBO and ![]() DEO (in orange) both share
arc OD.
DEO (in orange) both share
arc OD.
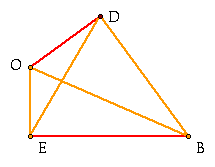
Therefore, ![]() DBO =
DBO = ![]() DEO (
DEO (![]() ABF =
ABF = ![]() DEA). Now look
at triangle ABF.
DEA). Now look
at triangle ABF.
We know that triangle ABF is a right triangle,
since F is one of the perpendiculars and therefore a right angle.
Due to this fact we know that ![]() A and
A and ![]() B must therefore
add to 90 degrees (
B must therefore
add to 90 degrees (![]() A and
A and ![]() B are complementary).
B are complementary).
Now look at the figure below:
We additionally can see that since ![]() E
forms a right angle, we know that
E
forms a right angle, we know that ![]() BED must be complementary
with
BED must be complementary
with ![]() DEA. Now since above we showed that
DEA. Now since above we showed that ![]() ABF (
ABF (![]() DBF) was equal
to
DBF) was equal
to ![]() DEA (
DEA (![]() DEO), we must conclude that
DEO), we must conclude that ![]() DEB =
DEB = ![]() A. This is the
first part of what we needed to show.
A. This is the
first part of what we needed to show.
Now we are half way done. Using this same
process we can now look at quadrilateral FOEC. In doing this we
will see that ![]() A =
A = ![]() FEC, as shown below.
FEC, as shown below.
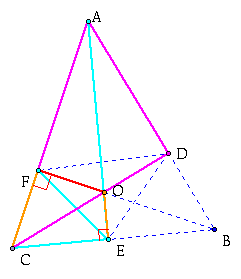
This figure is a combination of all the steps above. Click here to see a progression of these steps. Following these through will give us
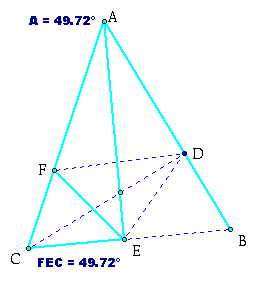
So now we know that ![]() A =
A = ![]() FEC =
FEC = ![]() DEB.
DEB.