This essay will discuss inscribing a triangle within an acute triangle with the least possible perimeter. This triangle is called the altitude triangle. This problem was thought of by the mathematician, Hermann Amandus Schwarz.
Let's start with an acute triangle ABC
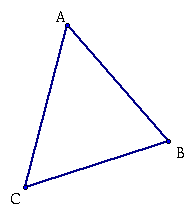
We want to end up with triangle DEF, inscribed inside the acute triangle ABC. As shown below:
Now by inscribed we mean that each of the vertices of the inscribed triangle DEF are on the sides of the orginal triangle ABC.
Please note there are at least two different proofs for this method, however in following with Schwarz we will revert to his proof.
The first part of the proof it to show the Theorem of Reflection. Click here.
When this is done, we have the following:
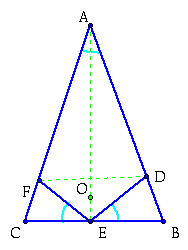
This result no enables the reflection
property of the altitude triangle to be used. So we can know state
things like 
CFE = AFE, and so on for the other angles.
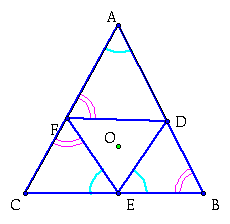
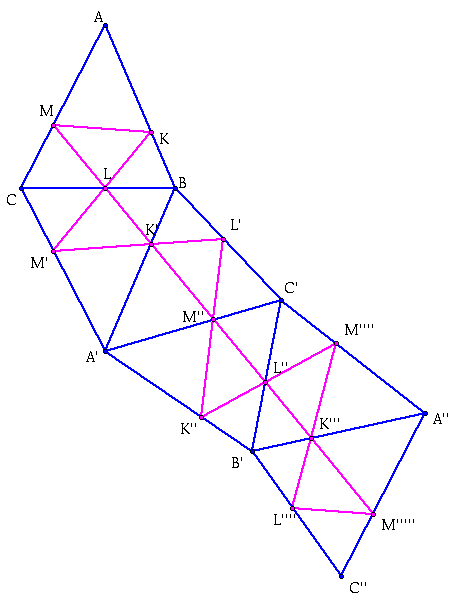
We are now ready to finally prove the minimum property for the altitude triangle. Click here to see the steps for the proof.
Essay idea taken from What is Mathematics: An Elementrry Approach to Ideas and Methods by Richard Courant and Herbert Robbins. 2nd edition, 1996.