

Let us start by looking at triangle ABC
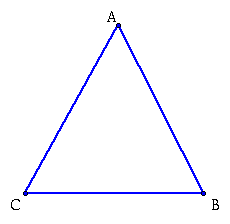
We must first inscribe an altitude triangle KLM into this triangle.

Now we are going to reflect the whole figure over the segment BC.
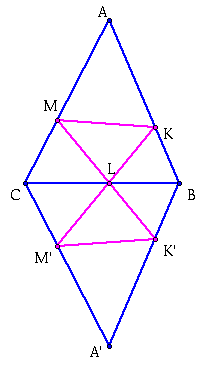
Now we are going to reflect this resulting triangle over segment BA'.
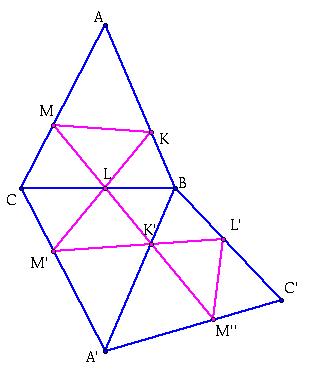
Now we are going to continue with this pattern till I have reflected three more times, giving the following image:
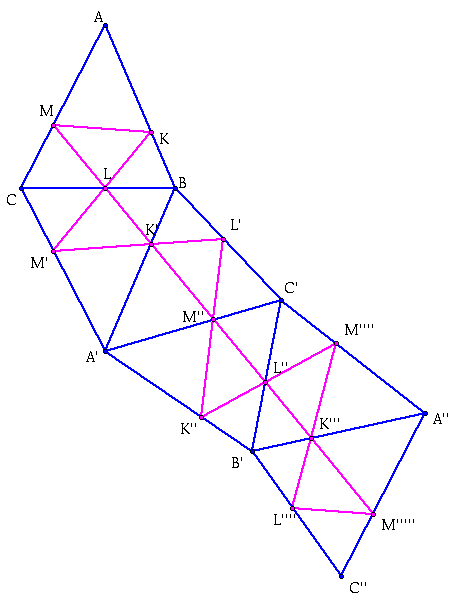
So now what we have six congruent triangles with the altitude triangle inscribed and all congruent. In the beginning triangle, side AC is now parallel to the final triangle, side A''C''. (Since in the first reflection side AC is rotated clockwise through an angle 2c, then through 2A, and in the third triangle not affected, fourth triangle 2c, counterclockwise, and then in the five triangle 2A counterclockwise which added together is a total of zero and thus parallel).
Now, due to the reflection property with the altitude triangle the striaght line segment MM''''', is twice the perimeter of the altitude. (since the turns make up the inside segments, as shown below).
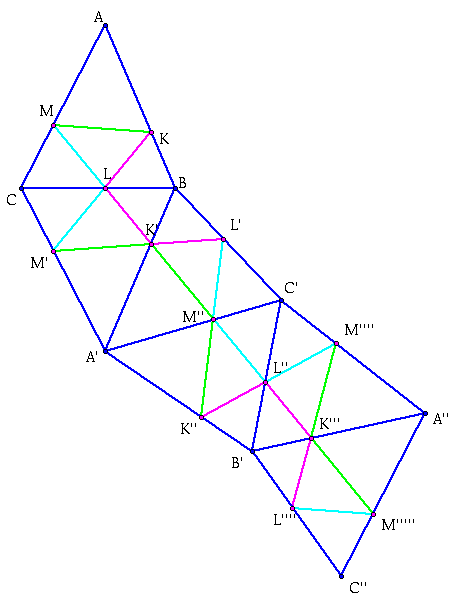
Now to prove that the altitude triangle is the shortest possible triangle we must take another inscribed triangle, triangle NOP, and follow the same process.
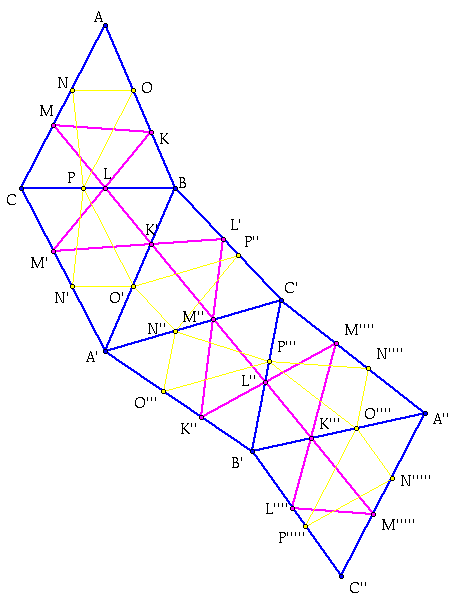
As one can see, no matter what path is taken from N to N''''', it will not be straight and therefore not the shortest path. So the only straight line is formed using the perpendiculars of the original triangle, forming the altitude triangle.