

When one thinks of the study of polyhedra, the Greek's geometry, usually comes to mind. However it was Descartes and Euler how discovered the following:
By a polyhedron is meant a solid whose surface consists of a number of polygonal faces. In the case of the regular solids, all the polygons are congruent and all of the angles at vertices are equal. A ployhedron is simple if there are no "holes" in it, so that its surface can be deformed continuously into the surface of a sphere.
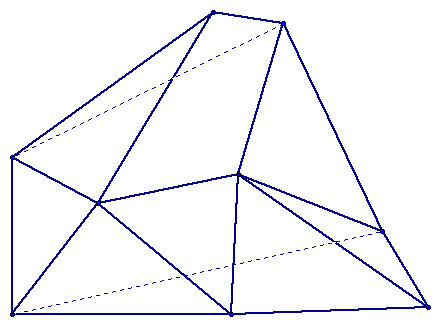
The figure below is a simple polyhedron. (This is not regular) Click here if you do not see the formula.
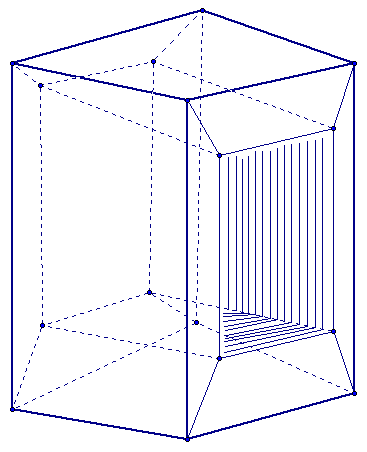
The figure below is a polyhedron, but is not simple. See the lines in the middle of the front rectangle, these are holes.
To ensure understanding, take a look at the following figures. (Click on them if you do not see it or want to check it.)
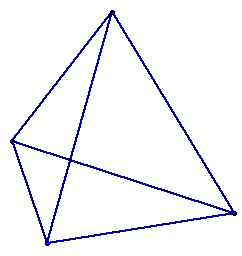
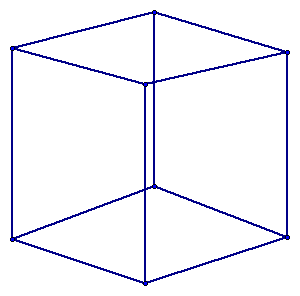
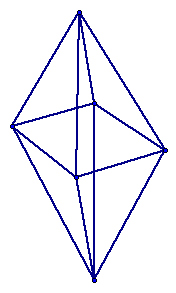
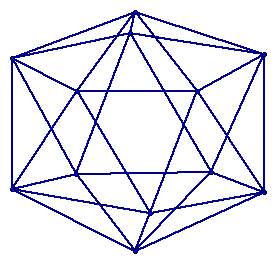
Now to prove Euler's formula, click here.
Essay idea taken from What is Mathematics: An Elementrry Approach to Ideas and Methods by Richard Courant and Herbert Robbins. 2nd edition, 1996.