

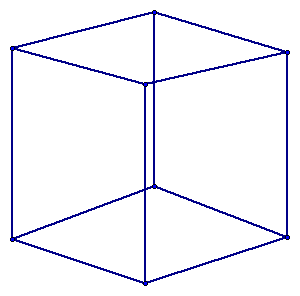
To start the proof of Euler's formula, let us think about a simple polyhedron that is hollow and the surface is made of thin rubber. If we cut out the faces and the angles between the edges, we will have changed this process. However the network of vertices and edges in the plane will be the same number as it was in the orginal polyhedron. The number of polygons, however will be one less than that of the orginal polyhedron (since one face was removed). We shall now show that for the plane network, V - E + F = 1, so that, if the removed face is counted, the result would be V - E + F = 2.
The first step is to "triangulate" the plane network in the following way:
In some polygon of the network which is not already a triangle we draw a diagonal.
The goal of creating diagonals is to increase both E and F by 1, thereby perserving the value of V - E + F. So we continue drawing diagonals joining pairs of points until the figure consists entirely of triangles, as it must eventually.
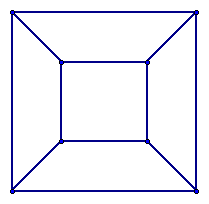
In the triangulated network, V - E + F has the value that it had before the division into triangles, since the drawing of diagonals has not changed it. Some of the triangles have edges on the boundary of the plane network.
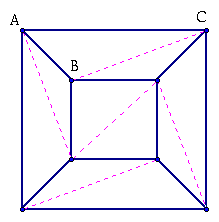
Of these some, such as ABC, have only one edge on the boundary, while other triangles may have two edges on the boundary. We want to take any boundary triangle and remove that part of it which does not also belong to some other triangle.
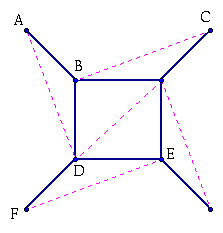
Thus, from ABC we remove the edge AC and the face, leaving the vertices A, B, C and the two edges AB and BC. With this new form though we have formed triangle DEF. If we remove the face, the two edges of DF and FE, and the vertex F. The removal of a triangle of type ABC decreases E and F by 1, while V is not affected, so the formula V - E + F is still unchanged.
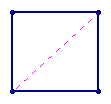
The removal of triangle DEF (or the like) decreases V by one, E by two, and F by 1, so the formula V - E + F is also not affected by this move. By a properly chosen swquence of these operations we can remove triangles with edges on the boundary until finally only one triangle is left with three edges, three vertices, and one face. (V - E + F = 1 => 3 - 3 + 1 = 1)
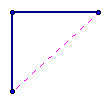
By this process we can see that the formula is unchanged when we take away triangles and therefore the original figure must equal one when it is missing one face. Therefore we know can conclude that by adding on face, the formula would equal two. QED.