We examine closely, the pedal triangle
DEF.
As you see below, the parent triangle ABC , along with arbitrary
pedal point H, allow for the pedal
triangle's existance and situational characteristics.
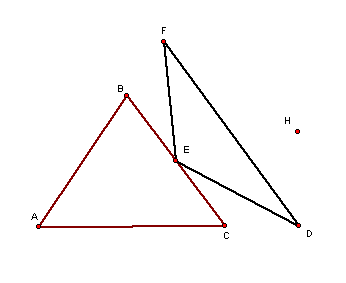
Point H is the pedal point of the pedal triangle and
is informally: the point of
intersection of the lines that are perpindicular or normal
to the extended lines that contain the
segments of the triangle. Remark : The normal
lines can be established anywhere along the lines
conatining the sides of the triangle even inside
the triangle.
To play and manipulate the pedal triangle click
here
To create your own pedal triangle click
here
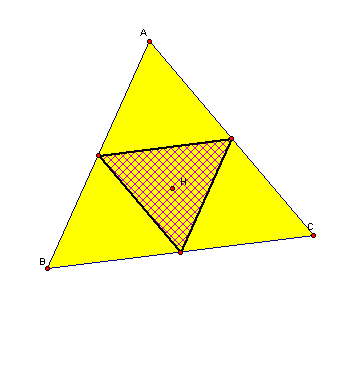
Here is the special case were the Pedal Point H is
the orthocenter and of course inside
the triangle. In actuality the orthocenter is always
a special pedal point to what could
be a pedal triangle.
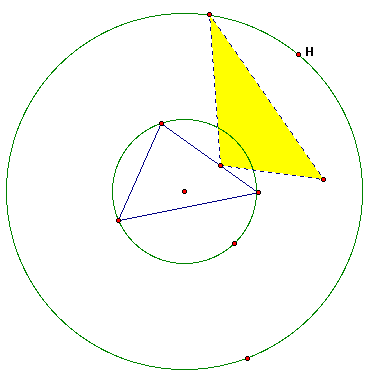
Below you see the pedal triangle and the pedal point
on a larger circle
Click here to watch animate,
watch and, augment the above situation
If you trace one of the midpoints you
will notice an ellipse if you trace all the
midpoints you will have individual
ellipses
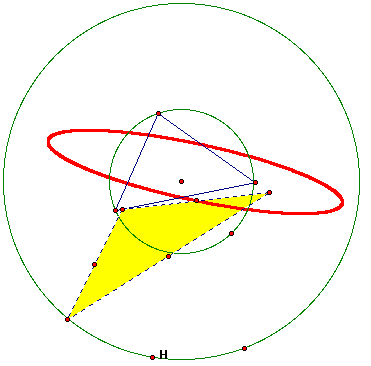
What will occur if we rotate H the same dirction, and
trace the midpoints of the triagle created from
the midpoints of the pedal triangle?
Click here to see
As we see from various manipulations the pedal triangle
maintains many special
relationships with its parent triangle.
Click here to
construct a derivative concept of the pedal triangle and attempt
to see their
similarities.
Return