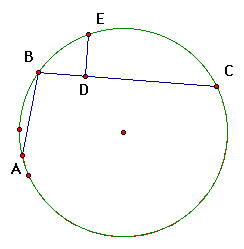
First, let us recall the theorem and the diagram of the theorem.
Given: BC > AB and E the midpoint of arc ABC.
Prove: AB + BD = DC

Now, let's use GSP to measure the segments, AB, BD and DC, and to calculate the sum of AB and BD. Doing this, we find the following results.
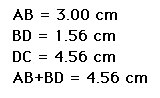
So, we find that for this example that the theorem holds. So, try moving C to another point on the circle and see what happens.
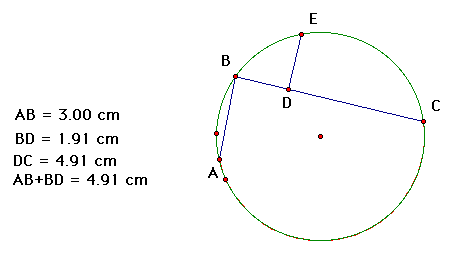
Again, the theorem holds. So, what happens if A is moved? So, use GSP to find out.
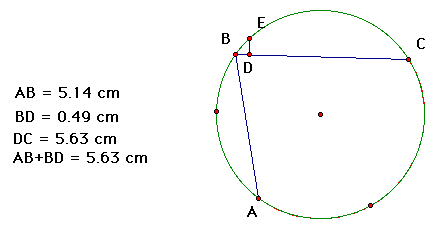
Notice, that this moves D closer to B, but again the theorem holds.
Hopefully, these examples have convinced you that the theorem holds. If you are still not convinced of this fact, click here to open a GSP sketch that will allow you to move the points. Just remember that AB < CB and that neither A nor C can go past point P. P is used to construct E and may also be moved.
Back to the Broken Chord Main Page