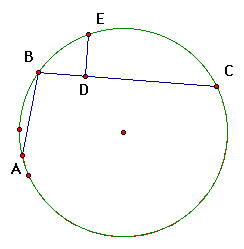
This paper will explore the Theorem of the Broken Chord. The Theorem of the Broken Chord states the following.
Given: BC > AB and E the midpoint of arc ABC.
Prove: AB + BD = DC

The paper will be broken into three parts. First, I will attempt to convince the reader that the theorem is true using Geometer's Sketch Pad. This will in no means be a proof, but hopefully it will help to show that the theorem is correct and convince the reader that it should be able to be proven.
Click here to be convinced and to hopefully see how examples and technology can help to clarify the problem for students.
Second, I will prove the Theorem of the Broken Chord.
Click here for the proof of the theorem.
Finally, we will look at some extensions of the theorem. Specifically, how the theorem leads to some of the trigonometric identities.
Click here for the extensions.
If you are unable to reconstuct the picture on your own.
Click here for a GSP sketch and script.
Return to Dr. Wilson's Homepage