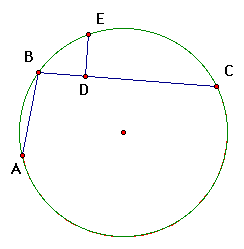
Again, recall the the theorem and the diagram.
Given: BC > AB and E the midpoint of arc ABC.
Prove: AB + BD = DC

First, Construct a circle with a radius of AB and a center at C. This now creates a segment CG congruent to segment AB. This can be seen in the following picture.
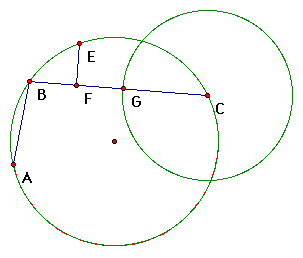
Second, constuct segments so that we have the triangles ABE and CGE.
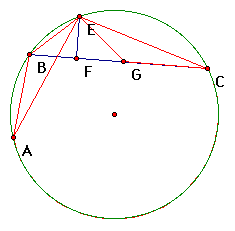
Now, these triangles can be proven congruent by SAS.
First, segments AB and CG are congruent because we constructed CG congruent to AB in the step above.
Second, angles A and C are congruent because they both intersect minor arc BE and angles that intersect the same arc are congruent.
Finally, remember that E is the midpoint of arc AEC. So, minor arcs AE and EC are congruent. Thus, segments AE and EC are congruent because chords that intersect congruent arcs are congruent.
Therefore, triangles ABE and CGE are congruent by SAS.
Third, prove triangles EBF and EFG congruent by HL.
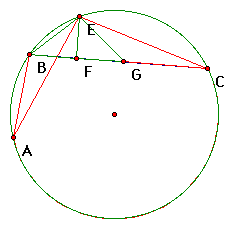
First, remember that EF is perpendicular to BC; so the triangles are right triangles which allows us to use Hypotenuse-Leg.
Second, segment EF is congruent to itself by the reflexive property.
Third, segments BE and GE are congruent by CPCTC.
Therefore, triangles EBF and EFG are congruent by HL.
Finally, we have enough information to prove AB + BF = FC.
First, FG + GC = FC because the sum of the parts equals the whole.
Second, AB + BF = AF because the sum of the parts is equal to the whole. If this is not obvious, look at the following picture.
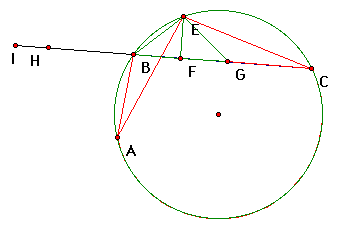
Here, BC has been extended to the point I. Then, segment BH has been constructed congruent to segment AB. Now, HB + BF = HF because the sum of the parts is equal to the whole. Then, we would substitute AB for HB which would give us AB + BF = HF.
Third, segment BF is congruent to segment FG by CPCTC. So, we substitute BF for FG and have the statement that BF + GC = FC.
Fourth, remember that segments AB and GC are congruent. This yields our last substitution which is AB for GC which gives us the following statement:
Return to the Broken Chord Main Page