
Consider the given problem. The center of the desired
circle will lie along a line from the center of
the given circles with the specified point.
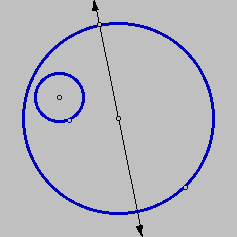 We need to find another locus for the center of the
tangent circle. Consider the problem as solved.
We need to find another locus for the center of the
tangent circle. Consider the problem as solved.
We would have this configuration:
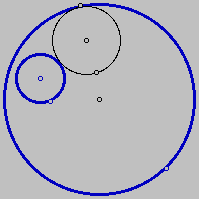 Then, if we added the lines through the centers,
Then, if we added the lines through the centers,
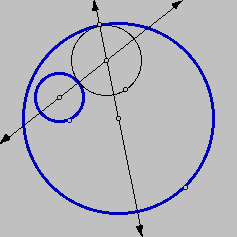 we would have this situation. Now consider the segment
from the center of the desired circle to
we would have this situation. Now consider the segment
from the center of the desired circle to
the center of the second given circle.
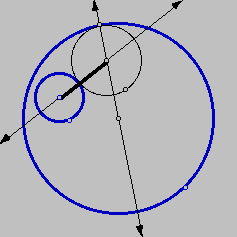 This segment is always of length the sum of the radius
of the desired circle plus the radius of the
This segment is always of length the sum of the radius
of the desired circle plus the radius of the
given circle that did not have a specified point. The same distance
can be laid off along the line
through the given point from the center of the desired circle,
by constructing an additional circle of
the same radius with center at the designated tangent point:
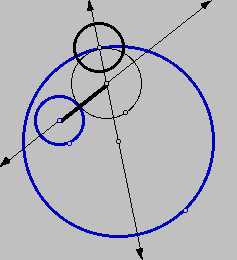 Now, an isosceles triangle is formed, like so,
Now, an isosceles triangle is formed, like so,
 and therefore the center of the desired tangent circle
lies along the perpendicular bisector of the
and therefore the center of the desired tangent circle
lies along the perpendicular bisector of the
base of this isosceles triangle, as follows, and now we have a
construction of the desired circle.
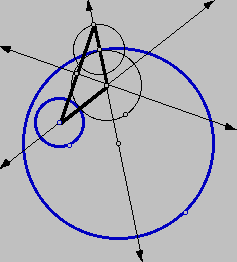
That is, construct a line through the center of the circle with
the designated point of tangency and
construct a circle of the same radius as the second of the given
circles with the designated point as
center. The intersection of the line and circle will allow construction
of the base of the isosceles
triangle and hence allow location of the center of the desired
circle. The construction follows.
Return








