

For this assignment, we were to explore the following: Given two circles, find a third circle that is tangent to the other two circles. For step by step instructions of how to find this circle, click here. Below is an example of the desired circle, it will be in red.
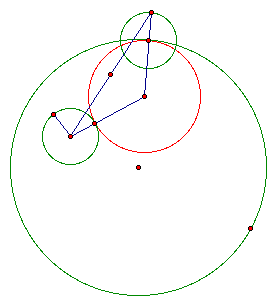
I found two things that I thought was quite interesting that I will discuss in this assignment.
The first is that if a segment is drawn from the center of the tangent circle to the centers of the two other circles, then it does not matter how you arrange the two circles, the total length of the segments remains constant. Explore this phenomenon by moving point A around the circle and notice that not only does the total length remain constant but that the total length is equal to the length of the radii of the two original circles.
The second thing that I thought was interesting was when I traced the locus of the center of the tangent circle. Below I will provide you with 5 different explorations and animations. Click on them and then click on animate point and notice the trace of the locus for each case.
One circle completely inside the other circle where their centers line up
One circle completely inside the other circle
One circle completely inside the other circle with them tangent
Two circles intersect at two points
Two circles not intersecting and with one not inside the other
Notice that their are three different shapes that are made. For the first, the trace of the locus forms another circle. For the middle three, an elipse is formed. For the last, an hyperbola is formed.