

This assignment is an investigation of pedal points and pedal triangles. The following are instructions on how to find the pedal point and pedal triangle. Let triangle ABC be any triangle. Then choose any point P that is in the plane. Construct perpendiculars from P to the sides of triangle ABC, and label these points of intersection R,S, and T. Connecting these three points, R, S, and T, the pedal triangle RST is formed for the Pedal point P. Two examples follow:
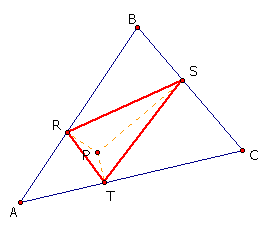
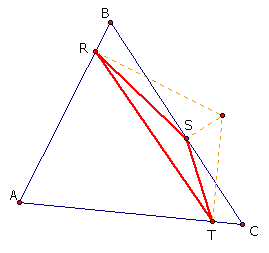
The problem that I will explore is the following:
Construct the incircle of triangle ABC(with triangle ABC acute to start with). To find the incenter, locate the point of concurrency of the angle bisectors of triangle ABC and then construct perpendiculars from the incenter to the sides of triangle ABC. The circle constructed by using the incenter as the center and one of the points of intersection of the perpedincular lines just constructed yields the incircle. When the incircle has been constructed, animate the Pedal point P about the incircle of ABC. Trace the loci of the midpoints of the sides. What curves result? To explore, click here and then click on animate point. Notice that the curves of the loci are all in the shape of an ellipse.
Now, let's see what happens to these curves when triangle ABC is a right triangle. Explore this in the same way as above.
What will the curves look like when triangle ABC is isosceles? equiangular?
For a discussion of what these curves look like, click here.