By: Denise Natasha Brewley and Venki Ramachandran

The definition of a Pedal Triangle is as follows:  Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.

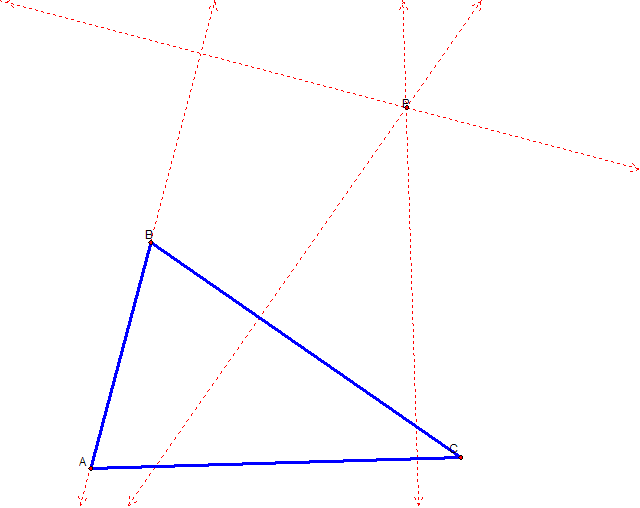
We begin this investigation by constructing a triangle ABC and a random point P in the plane.  We then construct perpendicular lines that pass through each line segment of ABC, namely, AB, AC, and CB.  The perpendicular line did not directly intersect line segment AB, we had to extend AB and then construct the perpendicular.

Notice that there is an intersection point of each perpendicular line through each segment.  I then identified each of these points and constructed triangle RST.  RST is our Pedal Triangle and the point P is our Pedal Point. 

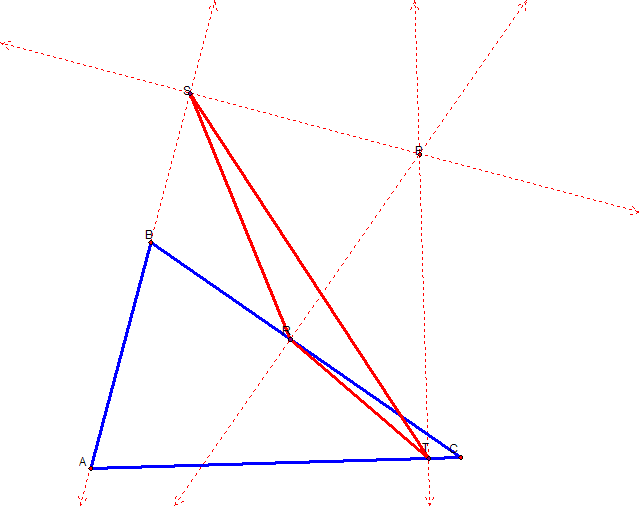
I then hid the dashed lines and explored the pedal triangles for various triangles and points that we are already familiar with.  Click here to open Geometer Sketch Pad and explore various locations of the pedal point, P. 

The primary focus of this investigation will be to explore what happens when pedal point P is on one of the segments of its parent triangle ABC.  We will also observe the PEDAL triangle and the SIMPSON line.

Investigation of side BC:

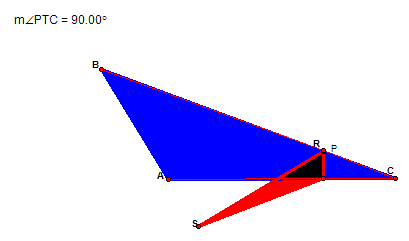
We will begin by looking at what happens when P is on side BC.  As bring the pedal point onto side BC, point P becomes point R from the Pedal triangle.  During this exploration I got a bit excited because it appeared that angle SBP was a right angle.  Unfortunately, when I varied the size of ABC this didn't hold up.  But what I did discover is that angle PTC is in fact a right angle.  If triangle ABC is varied it still holds true.  I looked at three cases -- when ABC is acute, obtuse, and a right triangle.  In the case when ABC is a right triangle, another interesting thing emerged -- angle SRT was also a right triangle. 

Investigation of side AB:

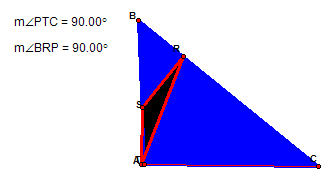
I then explored the case when the pedal point is on side AB. In this case point P becomes point S from the Pedal triangle.  I proceeded to explore in the same manner as in the first case.  Again, using the acute triangle, obtuse triangle and the right triangle cases. When ABC is an acute triangle, angle PTA is a right angle.  For clarity, remember that point P and point S are the same.  In the obtuse case angle BRP is right.  And last in the right triangle case, angle BRP is a right triangle. 

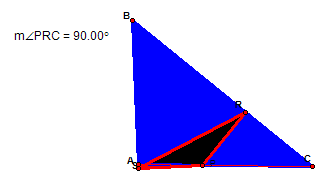
Investigation of side AC:

Based on the last two investigations, can you guess what happens to point P when it is placed on side AC?  You guessed it, point P becomes point T from the Pedal triangle.  An interesting observation is, for each case that I explored, the acute, obtuse and right triangle, angle PRC is a right triangle.  For the right angle case, I thought that the following would be right angles -- angle ASP, angle SBR, and angle PRS.  But they were not.  

Simpson Line Investigation:

The PEDAL triangle assumes different shapes and even collapses into a line (the SIMPSON'S line) depending on its location with reference to the parent triangle. Click here to see how the positions changes.

Return to DNB's page        Return to VRam's page