
A Proof of Congruent Circumcircles
By
Ken Montgomery

Figure 1: ![]()
![]() ,
,![]() , and
, and![]() are constructed in red (Figure 2).
are constructed in red (Figure 2).

Figure 2: ![]() with orthocenter, H
with orthocenter, H
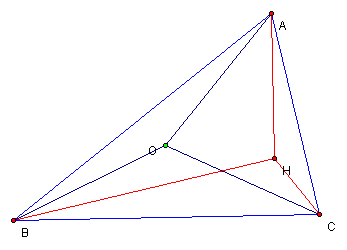
Figure 3: ![]() with orthocenter, H and circumcenter, O
with orthocenter, H and circumcenter, O
![]() is then constructed in purple (Figure 4).
is then constructed in purple (Figure 4).

Figure 4: ![]() with circumcircle in purple
with circumcircle in purple
![]() (Figure 5).
(Figure 5).
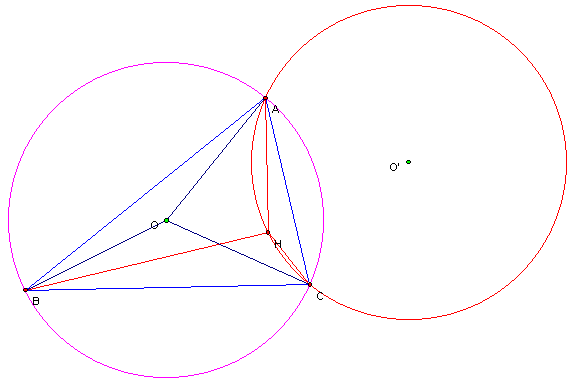
![]() with circumcenter, O’ and circumcircle in red
with circumcenter, O’ and circumcircle in red
![]() ,
,![]() ,
,![]() and
and ![]() are mutually congruent. We prove this as a theorem.
are mutually congruent. We prove this as a theorem.
![]() ,
,![]() ,
,![]() and
and ![]() are congruent
are congruent
We first construct the segments, ![]() and
and![]() (Figure 6).
(Figure 6).
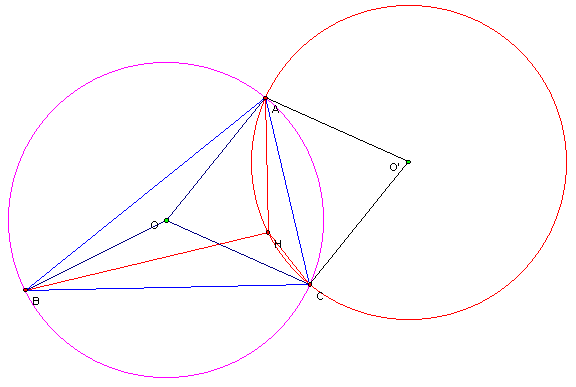
Figure 6: ![]()
![]() and
and ![]() , then by definition, both circumcenters, O and O’ lie
on the perpendicular bisector of AC (Figure 7).
, then by definition, both circumcenters, O and O’ lie
on the perpendicular bisector of AC (Figure 7).

Figure 7: O and O’ both lie on the
perpendicular bisector of ![]()
Quadrilateral COAO’ is formed by segments CO, OA, AO’ and
O’C. The diagonals of the quadrilateral are AC and OO’. Since ![]() , quadrilateral COAO’ is a rhombus and by definition
we have
, quadrilateral COAO’ is a rhombus and by definition
we have![]() . Since OA is the radius of the circumcircle for
. Since OA is the radius of the circumcircle for![]() and O’A is the radius of circumcircle for
and O’A is the radius of circumcircle for ![]() , the circumcircles are congruent and without loss of
generality, the circumcircles for
, the circumcircles are congruent and without loss of
generality, the circumcircles for ![]() ,
,![]() ,
,![]() and
and ![]() are also congruent (Figure 8).Ò
are also congruent (Figure 8).Ò
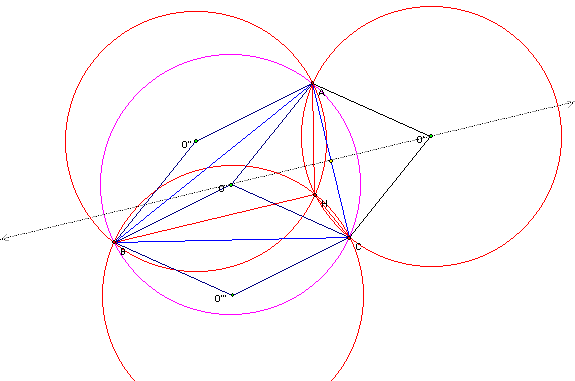
Figure 8: The circumcircles for ![]() ,
,![]() ,
,![]() and
and ![]() are congruent
are congruent
Return to Homepage