
A Proof of Ceva’s Theorem
By
Ken Montgomery
Ceva’s
Theorem:
![]() ,
,![]() and
and![]() intersect
in one point, T if and only if:
intersect
in one point, T if and only if:![]()
Proof:
Case 1: T
lies inside ![]()
Let D
lie on ![]() ,
E lie on
,
E lie on![]() ,
F on
,
F on ![]() and
let
and
let![]() ,
,![]() and
and![]() intersect
at T (Figure 1).
intersect
at T (Figure 1).
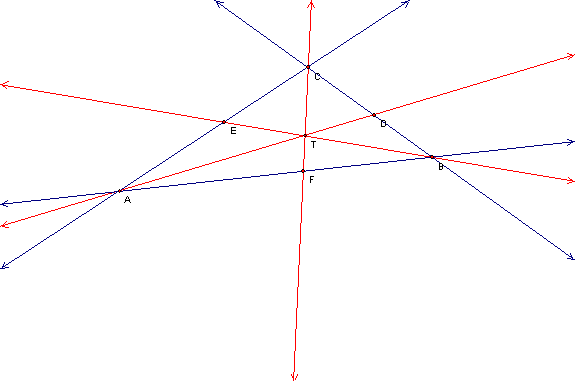
Figure 1: ![]() ,
with T in the triangle’s interior
,
with T in the triangle’s interior
Then, we have
that:
![]()
However,
![]()
and since
![]()
we obtain
![]()
Likewise, for
side![]() ,
we have:
,
we have:
![]()
but since,
![]()
and since,
![]()
we have
![]()
Furthermore,
for side![]() we
also have:
we
also have:
![]()
but since,
![]()
and since,
![]()
we have
![]()
Therefore, we
have
![]()
Conversely,
assume that
![]() .
.
For each point,
M on![]() ,
and only for points on
,
and only for points on![]() ,
we have that
,
we have that
![]()
Further, the
line![]() consists
of points N, satisfying the equation:
consists
of points N, satisfying the equation:
![]()
Also,![]() consists
of points O, satisfying the equation:
consists
of points O, satisfying the equation:
![]()
Let T be the
point of intersection of![]() and
and![]() .
Thus,
.
Thus,
![]()
and we have
![]()
so T
lies on![]() also.
also.
Case 2: Without
loss of generality, let T lie on the opposite side of![]() from
C.
from
C.
Let D
lie outside of ![]() ,
E lie outside of
,
E lie outside of![]() ,
F on
,
F on ![]() and
let
and
let![]() ,
,![]() and
and![]() intersect
at T (Figure 2).
intersect
at T (Figure 2).
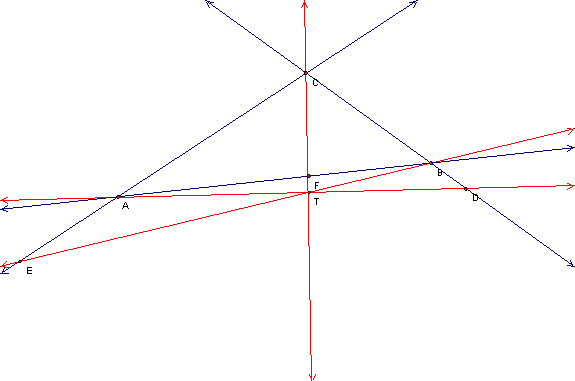
Figure 2: ![]() ,
with T opposite of
,
with T opposite of ![]() ,
from C
,
from C
Then, we have,
for side![]() that:
that:
![]()
However, since
![]()
and since
![]()
we have
![]()
Likewise, for
side![]() we
have that:
we
have that:
![]()
However, since
![]()
and since
![]()
we have
![]()
Also, for side![]() ,
we have that:
,
we have that:
![]()
However, since
![]()
and since
![]()
we have
![]()
Therefore, we
have the equation
![]()
Conversely,
assume that
![]()
then it is also
true that
![]()
For each point,
M on![]() ,
and only for points on
,
and only for points on![]() ,
we have that
,
we have that
![]()
Further, the
line![]() consists
of points N, satisfying the equation:
consists
of points N, satisfying the equation:
![]()
Also,![]() consists
of points O, satisfying the equation:
consists
of points O, satisfying the equation:
![]()
Let T be the
point of intersection of![]() and
and![]() .
Thus,
.
Thus,
![]()
and we have
![]()
so T
lies on![]() also.
also.
Return to Homepage