Day 7 Lines Intersecting
Inside or Outside a Circle
If
two lines intersect a circle, there are three places where the lines can
intersect.
You
know how to find the angle and arc measures when lines intersect on the circle. Now we’ll examine theorems that help us to
find measures when the lines intersect inside
or outside the circle.
1ST Theorem:
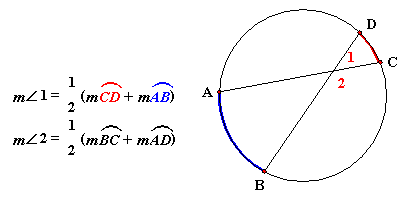
If two chords intersect in the interior of a circle, then
the measure of each angle is one
half the sum of the
measures of the arcs intercepted by
the angle and its vertical angle.
Proof:
An
angle formed by a secant segment and a tangent to a circle is called a secant-tangent
angle. The next theorem involves
secant-tangent angles.
CASE I
If a tangent
and a secant intersect in the exterior
of a circle,
then the
measure of the angle formed is one half the difference
of the
measures of the intercepted arcs.
Proof:
A tangent-tangent angle is
the angle formed by two tangents to a circle. The following theorem involves the measurement
of the tangent-tangent angle.
If two
tangents intersect in the exterior of
a circle,
then the measure of the angle
formed is one half the difference
of the measures of the intercepted
arcs.
Proof:
The angle formed when two secants
intersect is a secant angle. This
last theorem looks at the measurement of the secant angle.
If two
secants intersect in the exterior of
a circle,
then the measure of the angle
formed is one half the difference
of the measures of the intercepted
arcs.
Proof:
