Proof of the Ratios = 4

By: Ginger Rhodes

Given: P is inside of triangle ABC, P is the centroid

Prove: the ratio of the areas of triangle ABC and triangle DEF equals 4

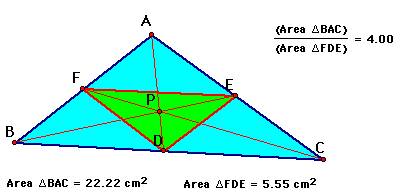
First, to make it easier to discuss I will label AB = x, AC = y, and BC = z. Now, F, E, and D are the midpoints of the sides of the triangle, and therefore FE, FD, and DE are parallel to the respective side and are half the length of the sides. So FE = 1/2 z, FD = 1/2 y, and DE = 1/2 x.

Using Heron’s formula the area of triangle ABC is

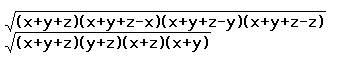
and the area of triangle FED is

Now, Triangle ABC / Triangle FED = 4

RETURN