Final Assignment

By: Ginger Rhodes

Part A: Consider the triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F, respectively.

To explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P click HERE. What do you notice about the two numbers?

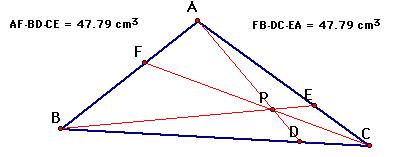
The numbers are the same!!

Part B: From Part A explorations I conjecture

To see a proof click HERE.

Now, what do you think happens if P is in the exterior of the triangle? Click HERE to explore.

Part C: Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4? Click HERE to explore.

The ratio of the areas appears to equal 4 when P is the centroid. Click HERE for a proof.

RETURN