
Proof of the Simpson
Line
By: Ginger Rhodes
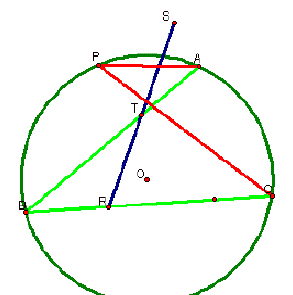
Given: DABC is inscribed in
circle O, The Pedal point P is on the circle O, PS^AC, PT^AB, and PR^BC [These are segments]
Prove: Points R, S, and T, the Simpson line, are
collinear
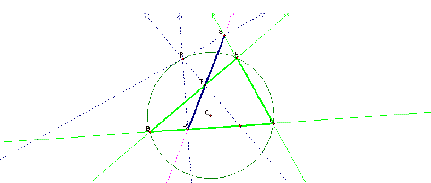
Proof:
<PSA and <PTA are both right
angles, and therefore supplementary. So <SPT and <TAS are supplementary
and opposite angles in Quadrilateral PSAT are supplementary.
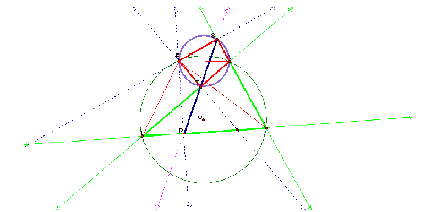
Now,
<PST
and <PAT
have the same intercepted arc, which means the angles are congruent. Similary,
points P, R, C, and S are cyclic.
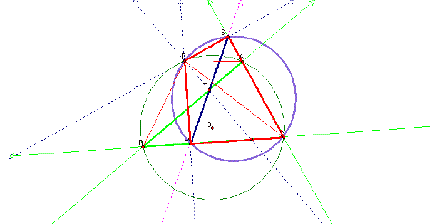
So,
<PCR
and <PSR
have the same intercepted arc, which means the angles are congruent.
By
hiding some of the lines it is easier to see DPAB@DPCB [same intercepted
arcs].
So, <PST congruent
<PAT, <PCR congruent
<PSR, and <PAB congruent <PCB.
Notice, <PAB is
another name for <PAT and <PCB is another name for <PCR.
Using the transitive property we can establish <PST @ <PSR, which
implies S, T, and R are collinear!