

Two cars are racing 500 miles on a 2 mile oval track. The first car averages 105 mph. The second car averages 120 mph but is delayed at the start by 30 minutes due to engine problems.
Begin by using the equation for distance to write the equation of a line for each car.
Now, write the equations in parametric form.
and
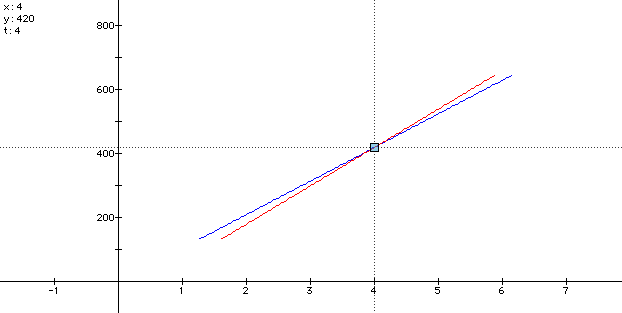
Now for the winner: the car with the smaller t value when y = 500 wins the race. Let's trace on our graph and see who wins.
Tracing Car 1's graph:
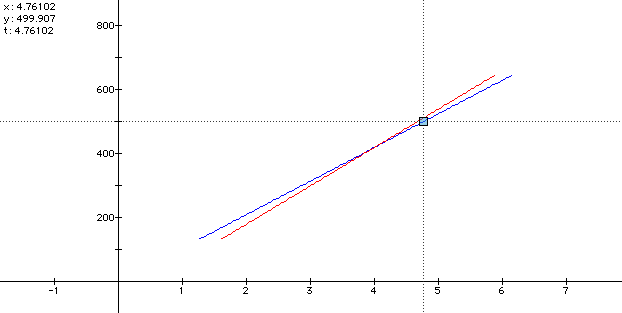
Tracing Car 2's graph:
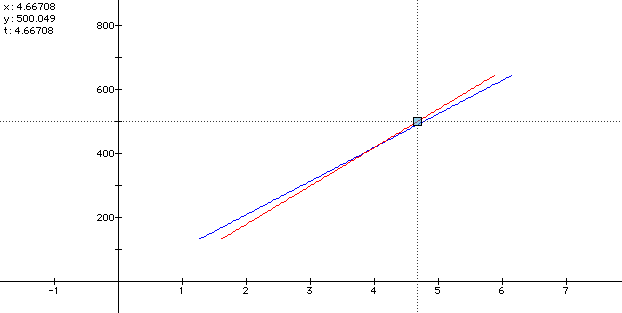
CAR 2 WINS!!