Writing a Parametric Equation

by Amy Benson

Problem: Write parametric equations of a line through (7, 5) with slope of 3. Graph the line using your equations.

The Equations

 

(x, y) = (7, 5) + (1, 3)t

where (7,5) is the time = 0 point and (1, 3) represents the rate of change as time increases.

Then,

x = 7 + t

and

y = 5 + 3t

These parametric equations would yield the following points:

(7, 5), (8, 8), (9,11), (10, 14), etc.

The Graph

 

In this case, the indicator is placed at t=0 and shows that the point is indeed (7,5),

A Different Approach
The Equations

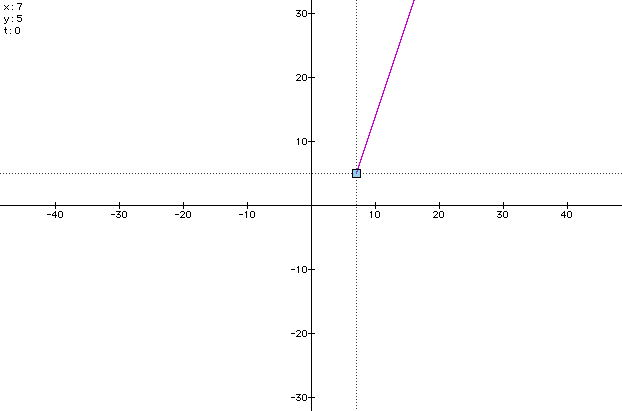
Instead of using the vector approach to this problem, let's try using the point-slope formula.

y - 5 = 3(x - 7)

y - 5 = 3x - 21

y = 3x - 16

Having found the line, we now write parametric equations of this line:

x = t

y = 3t - 16

The Graph

From this graph, we see that these are parametric equations through (7, 5) with a slope of 3.

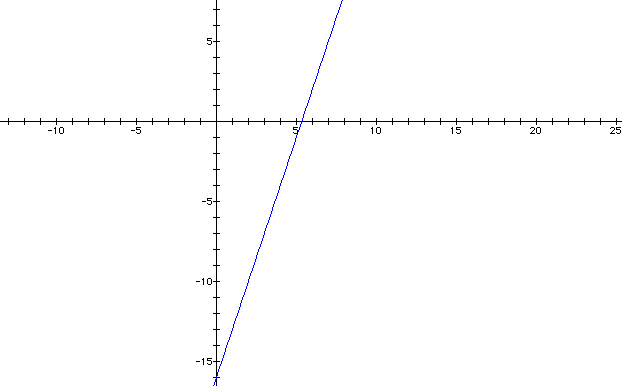
To use this strategy in a word problem, click here.

Return