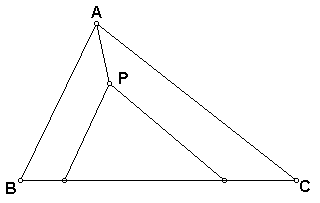

The Approach:
We want to trisect the area of triangle ABC from a point inside the triangle (call it P), extending two segments down from P onto BC and extending a segment up from P to A. We'll attempt to use some of the trisections we've already done to simplify this process.
Simplify the Problem:
We can simplify this problem greatly by drawing in the median of triangle ABC from A.
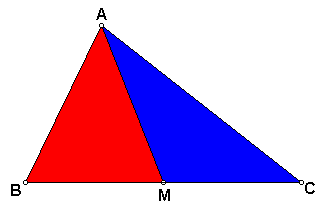
M is the midpoint of BC, so AM is the median of triangle ABC from A. We know that the median bisects the area of triangle ABC. So let's trisect triangle ABM using our parallel line trisection.
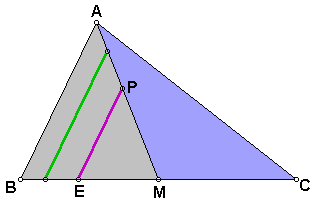
The goal of trisecting triangle ABM was to find out where to place our point P. If we use the top trisection line (the purple one- PE), then triangle PEM is 1/3 the area of triangle ABM. Since triangle ABM is 1/2 the area of triangle ABC, triangle PEM is 1/6 the area of triangle ABC. If we can somehow create a triangle on the other side of the median (AM) with the same area as triangle PEM, we will have our trisection from point P.
Finishing the Construction:
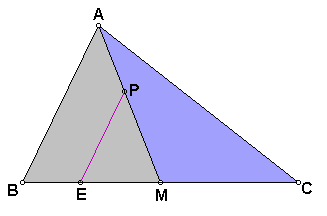
We have our point P, and we know that triangle PEM is 1/6 the area of triangle ABC. What we need to do is create a triangle on the other side of the median (AM) with the same area as triangle PEM.
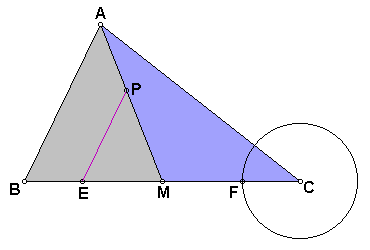
In order for our triangle on the other side of AM to have the same area as PEM, the other point on BC must be the same distance away from C as E is away from B. In order to construct this, all we need to do is create a circle centered at C with a radius the same length as BE. Therefore m(BE) = m(CF).
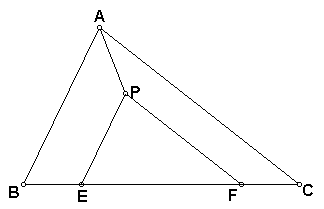
Now all we need to do is create segment PF and get rid of some extranneous line segments and we're done!
Seeing It All With GSP:
To check this construction out and see the areas measured, here is a GSP Sketch of this construction.